
【题目】如图,已知BC是⊙O的弦,A是⊙O外一点,△ABC为正三角形,D为BC的中点,M为⊙O上一点.
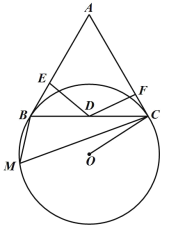
(1)若AB是⊙O的切线,求∠BMC;
(2)在(1)的条件下,若E,F分别是AB,AC上的两个动点,且EDF120,⊙O的半径为2,试问BECF的值是否为定值?若是,求出这个定值;若不是,请说明理由.
【答案】(1)60°;(2)BE+CF的值是定值,BE+CF=![]() .
.
【解析】
(1)连接BO,由AB是切线可以得到∠ABO的度数,由△ABC为等边三角形,得到∠OBC的度数,然后得到∠BOC,根据圆心角与圆周角的关系得到∠BMC的度数.
(2)作DH⊥AB于H,DN⊥AC于N,连结AD ,OD,如图2,根据等边三角形三角形的性质得AD平分∠BAC,∠BAC=60°,则利用角平分线性质得DH=DN,根据四边形内角和得∠HDN=120°,由于∠EDF=120°,所以∠HDE=∠NDF,接着证明△DHE≌△DNF得到HE=NF,于是BE+CF=BH+CN,再计算出BH=![]() BD,CN=
BD,CN=![]() DC,则BE+CF=
DC,则BE+CF=![]() BC,于是可判断BE+CF的值是定值,为等边△ABC边长的一半,再计算BC的长即可.
BC,于是可判断BE+CF的值是定值,为等边△ABC边长的一半,再计算BC的长即可.
(1)解:如图,连接BO,
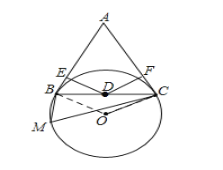
∵AB是圆的切线,
∴∠ABO=90°,
∵△ABC是等边三角形,
∴∠ABC=60°,
∴∠CBO=90°-60°=30°,
∵BO=CO,
∴∠BCO=∠CBO=30°,
∴∠BOC=120°,
∴∠BMC=![]()
(2)解:BE+CF的值是为定值.
理由:作DH⊥AB于H,DN⊥AC于N,连结AD,OD,如图2,
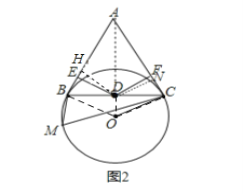
∵△ABC为正三角形,D为BC的中点,
∴AD平分∠BAC,∠BAC=60°,
∴DH=DN,∠HDN=120°,
∵∠EDF=120°,
∴∠HDE=∠NDF,
在△DHE和△DNF中,
∴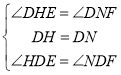 ,
,
∴△DHE≌△DNF,
∴HE=NF,
∴BE+CF=BH-EH+CN+NF=BH+CN,
在Rt△DHB中,∵∠DBH=60°,
∴BH=![]() BD,
BD,
同理可得CN=![]() OC,
OC,
∴BE+CF=![]() DB+
DB+![]() DC=
DC=![]() BC,
BC,
∵BD=![]() ,
,
∴BC=![]() ,
,
∴BE+CF=![]() ,
,
∴BE+CF的值是定值,为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,函数![]() 的图象G与直线l:y=﹣x+7交于A(1,a),B两点.
的图象G与直线l:y=﹣x+7交于A(1,a),B两点.
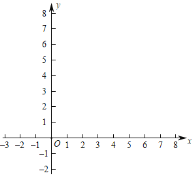
(1)求k的值;
(2)记图象G在点A,B之间的部分与线段AB围成的区域(不含边界)为W.点P在区域W内,若点P的横纵坐标都为整数,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果记y=![]() =f(x),并且f(1)表示当x=1时y的值.即f(1)=
=f(x),并且f(1)表示当x=1时y的值.即f(1)=![]() =
=![]() ;f(
;f(![]() )表示当x=
)表示当x=![]() 时y的值,f(
时y的值,f(![]() )=
)=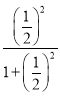 =
=![]() …,那么f(﹣1)+f(﹣2)+f(﹣
…,那么f(﹣1)+f(﹣2)+f(﹣![]() )+f(﹣3)+f(﹣
)+f(﹣3)+f(﹣![]() )+…+f(﹣2019)+f(﹣
)+…+f(﹣2019)+f(﹣![]() )=_____.
)=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,平行四边形ABOC的边OB在x轴上,过点C(3,4)的双曲线与AB交于点D,且AC=2AD,则点D的坐标为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度a为10 米),围成一个长方形的花圃.设花圃的宽AB为x米,面积为S平方米.
(1)求S与x的函数关系式;写出自变量x的取值范围.
(2)怎样围才能使长方形花圃的面积最大?最大值为多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC = 90°,BC = 1,AC =![]() .
.

(1)以点B为旋转中心,将△ABC沿逆时针方向旋转90°得到△A′BC′,请画出变换后的图形;
(2)求点A和点A′之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区准备五一组织社区内老年人去到县参加采摘节,现有甲、乙两家旅行社表示对老年人优惠,甲旅行社的优惠方式为:在原来每人100元的基础上,每人按照原价的60%收取费用;乙旅行社的优惠方式为:在收取一个600元固定团费的基础上,再额外收取每人40元.设参加采摘节的老年人有x人,甲、乙两家旅行社实际收费为![]() 元、
元、![]() 元.
元.
(Ⅰ)根据题意,填写下表:
老年人数量(人) | 5 | 10 | 20 | |
甲旅行社收费(元) | 300 | |||
乙旅行社收费)(元) | 800 |
(Ⅱ)求![]() 、
、![]() 关于x的函数关系式(不用写出自变量的取值范围)?
关于x的函数关系式(不用写出自变量的取值范围)?
(Ⅲ)如果![]() ,选择哪家旅行社合算?
,选择哪家旅行社合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
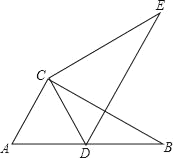
【题目】如图,在直角三角形ABC中,∠ACB=90°,将△ABC绕点C逆时针方向旋转,使点A落在AB边上的点D处,得到△DEC.
(1)点B的对应点是点 ,BC的对应线段是 .
(2)判断△ACD的形状.
(3)若AD=CD,求∠B和∠BCE的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com