
分析 由菱形ABCD中,对角线AC和BD相交于点O,∠BAD=120°,AB=15,可求得∠BAC的度数,AC⊥BD,根据直角三角形两锐角互余求出∠ABD的度数;然后利用含30°角的直角三角形的性质,求得OA与OB的长,继而求得AC与BD的长,则可求得菱形ABCD的面积.
解答  解:如图,∵菱形ABCD中,∠BAD=120°,
解:如图,∵菱形ABCD中,∠BAD=120°,
∴∠BAC=$\frac{1}{2}$∠BAD=60°,AC⊥BD,
∴∠ABD=90°-∠BAC=30°;
∵AB=15,
∴OA=$\frac{1}{2}$AB=7.5,
∴OB=$\sqrt{3}$OA=$\frac{15\sqrt{3}}{2}$,
∴AC=2OA=15,BD=2OB=15$\sqrt{3}$,
∴菱形ABCD的面积为:$\frac{1}{2}$AC•BD=$\frac{1}{2}$×15×15$\sqrt{3}$=$\frac{225\sqrt{3}}{2}$.
点评 此题考查了菱形的性质,含30°角的直角三角形的性质.此题难度不大,注意掌握数形结合思想的应用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
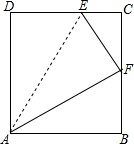 如图,在矩形ABCD中,E是DC上的一点,以线段AE为折痕对折,使点D落在BC边上的中点F处,且EF平分∠AEC,求证:AF是∠EAB的平分线.
如图,在矩形ABCD中,E是DC上的一点,以线段AE为折痕对折,使点D落在BC边上的中点F处,且EF平分∠AEC,求证:AF是∠EAB的平分线.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内切 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com