
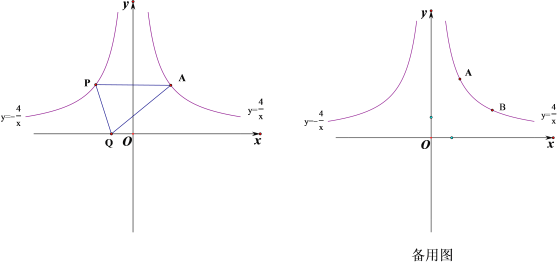
【题目】平面直角坐标系xOy中,已知函数y1=![]() (x>0)与y2=﹣
(x>0)与y2=﹣![]() (x<0)的图象如图所示,点A、B是函数y1=
(x<0)的图象如图所示,点A、B是函数y1=![]() (x>0)图象上的两点,点P是y2=﹣
(x>0)图象上的两点,点P是y2=﹣![]() (x<0)的图象上的一点,且AP∥x轴,点Q是x轴上一点,设点A、B的横坐标分别为m、n(m≠n).
(x<0)的图象上的一点,且AP∥x轴,点Q是x轴上一点,设点A、B的横坐标分别为m、n(m≠n).
(1)求△APQ的面积;
(2)若△APQ是等腰直角三角形,求点Q的坐标;
(3)若△OAB是以AB为底的等腰三角形,求mn的值.
【答案】(1)S=4(2)![]() (3)mn=4
(3)mn=4
【解析】试题分析:(1)由点A的横坐标为m,则A(m, ![]() ),P(-m,
),P(-m, ![]() ),过点P、A、Q分别作PM
),过点P、A、Q分别作PM![]() x轴交x轴于点M,PN
x轴交x轴于点M,PN![]() x轴交x轴于点N,QR
x轴交x轴于点N,QR![]() AP交AP轴于点R,可得出S矩形PMNA=8,由四边形PMQR和四边形ARQN是矩形可得:S△PQM=S△PRQ,S△ANQ=S△ARQ,所以S△APQ=S△PRQ+ S△ARQ=
AP交AP轴于点R,可得出S矩形PMNA=8,由四边形PMQR和四边形ARQN是矩形可得:S△PQM=S△PRQ,S△ANQ=S△ARQ,所以S△APQ=S△PRQ+ S△ARQ=![]() S矩形PMNA;(2)分情况讨论,当PQ
S矩形PMNA;(2)分情况讨论,当PQ![]() x轴时,求得
x轴时,求得![]() ,当PQ=AQ时
,当PQ=AQ时![]() ;(3)由OA=OB,解得mn=4.
;(3)由OA=OB,解得mn=4.
试题解析:
(1)过点P、A、Q分别作PM![]() x轴交x轴于点M,PN
x轴交x轴于点M,PN![]() x轴交x轴于点N,QR
x轴交x轴于点N,QR![]() AP轴交AP轴于点R,则四边形APMN、四边形PMQR、四边形ARQN是矩形,如图所示:
AP轴交AP轴于点R,则四边形APMN、四边形PMQR、四边形ARQN是矩形,如图所示:
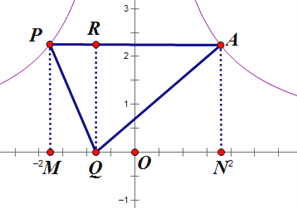
∵点A的横坐标为m,且在函数![]() 上,AP∥x轴,且点P在函数
上,AP∥x轴,且点P在函数![]() 上,
上,
∴点A(m, ![]() ),点P(-m,
),点P(-m, ![]() ),
),
∴MN=m-(-m)=2m,PM=![]() ,
,
∴S矩形PMNA=2m╳![]() =8,
=8,
∵四边形PMQR、四边形ARQN是矩形,
∴S△PQM=S△PRQ,S△ANQ=S△ARQ,
∴S△APQ=S△PRQ+ S△ARQ=![]() S矩形PMNA=4;
S矩形PMNA=4;
(2)当PQ![]() x轴时,则PQ=
x轴时,则PQ=![]() ,,AP=2m,
,,AP=2m,
∵PQ=AP
∴2m=![]() ,
,
∴m=![]()
∴![]() ,
,
当PQ=AQ时,则![]() ;
;
(3)∵△OAB是以AB为底的等腰三角形,
∴OA=OB,
∵A(m, ![]() ),B(n,
),B(n, ![]() ),
),
∴![]()
∴mn=4.


科目:初中数学 来源: 题型:
【题目】阅读可以增进人们的知识也能陶冶人们的情操.我们要多阅读,多阅读有营养的书.因此我校对学生的课外阅读时间进行了抽样调查,将收集的数据分成![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五组进行整理,并绘制成如图所示的统计图表(图中信息不完整).
五组进行整理,并绘制成如图所示的统计图表(图中信息不完整).
请结合以上信息解答下列问题
(1)求![]() ,
, ![]() ,
, ![]() 的值;
的值;
(2)补全“阅读人数分组统计图”;
(3)估计全校课外阅读时间在![]() 以下(不含
以下(不含![]() )的学生所占百分比.
)的学生所占百分比.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某牛奶加工厂现有鲜奶9吨,若在市场上直接销售鲜奶,每吨可获取利润500元;制成酸奶销售,每吨可获取利润1200元;制成奶片销售,每吨可获取利润 2000元。
该加工厂的生产能力是:如制成酸奶,每天可加工3吨;制成奶片,每天可加工1吨。受人员限制,两种加工方式不可同时进行。受气温条件限制,这批牛奶必须在4天内全部销售或加工完毕。为此,该厂设计了两种可行方案:
方案一:尽可能多地制成奶片,其余直接销售鲜奶;
方案二:将一部分制成奶片,其余制成酸奶销售,并恰好4天完成。
你认为哪种方案获利最多?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
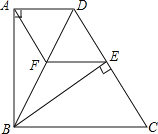
【题目】如图,四边形ABCD中,AD∥BC,BA⊥AD,BC=DC,BE⊥CD于点E.
(1)求证:△ABD≌△EBD;
(2)过点E作EF∥DA,交BD于点F,连接AF.求证:四边形AFED是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举办中学生足球赛,初中男子组共有市直学校的A、B两队和县区学校的e、f、g、h四队报名参赛,六支球队分成甲、乙两组,甲组由A、e、f三队组成,乙组由B、g、h三队组成,现要从甲、乙两组中各随机抽取一支球队进行首场比赛.
(1)在甲组中,首场比赛抽到e队的概率是 ;
(2)请你用画树状图或列表的方法,求首场比赛出场的两个队都是县区学校队的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
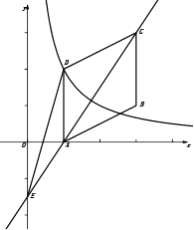
【题目】(本题满分10分)如图,在平行四边形ABCD中,点A、B、C的坐标分别是(1,0)、(3,1)、(3,3),双曲线y=![]() (k≠0,x>0)过点D.
(k≠0,x>0)过点D.
(1)求此双曲线的解析式;
(2)作直线AC交y轴于点E,连结DE,求△ CDE的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com