
【题目】如图,在平面直角坐标系内,点O为坐标原点,点A在x轴负半轴上,点B、C分别在x轴、y轴正半轴上,且OB=2OA,OBOC=OCOA=2.
(1)求点C的坐标;
(2)点P从点A出发以每秒1个单位的速度沿AB向点B匀速运动,同时点Q从点B出发以每秒3个单位的速度沿BA向终点A匀速运动,当点Q到达终点A时,点P、Q均停止运动,设点P运动的时间为t(t>0)秒,线段PQ的长度为y,用含t的式子表示y,并写出相应的t的范围;
(3)在(2)的条件下,过点P作x轴的垂线PM,PM=PQ,是否存在t值使点O为PQ中点? 若存在求t值并求出此时△CMQ的面积.

【答案】(1)点A的坐标为(-4,0),点B的坐标为(8,0),点C的坐标为(0,6)(2)见解析(3)8或16
【解析】
(1)由OBOC=OCOA=2可得OB﹣OA=4,结合OB=2OA可得出OA、OB的长度,从而得出OC的长度,写出点C的坐标即可;(2)分别求出P、Q两点相遇的时间、Q点到达A点的时间,写出不同的时间范围内,PQ的长度y与时间t的关系式即可;(3)O为P、Q的中点,即OP=OQ,将OP、OQ用含t的式子表示,列方程,解出t,然后画图,由于不确定M点位于x轴上方或者下方,所以进行分类讨论,利用割补法分别求出△CMQ的面积.
(1)∵OB﹣OC=OC﹣OA=2,
∴OB﹣OA=4,
∵OB=2OA,
∴OA=4,
∴OB=8,OC=6,
∴C(0,6);
(2)由(1)知:AB=OA+OB=12,
∵点P从点A出发以每秒1个单位的速度沿AB向点B匀速运动,同时点Q从点B出发以每秒3个单位的速度沿BA向终点A匀速运动,
∴点P运动的时间为t(t>0)秒时,AP=t,BQ=3t,
当P、Q两点相遇时的t的值为:12÷(1+3)=3秒,
∵当点Q到达终点A时,点P、Q均停止运动,
∴t的最大值为12÷3=4秒;
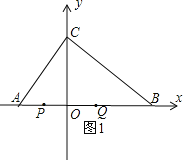
①当0<t≤3时,如图1,
PQ=AB﹣AP﹣QB=12﹣t﹣3t=12﹣4t,
即y=12﹣4t(0<t≤3);
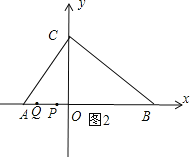
②当3<t≤4时,如图2,
PQ=AP+BQ﹣AB=4t﹣12,
即y=4t﹣12(3<t≤4);
(3)存在t值使点O为PQ中点,
∵点O为PQ中点,
∴0<t≤3,OP=OQ,即OA﹣AP=OB﹣BQ,
∴4﹣t=8﹣3t,解得:t=2,
当t=2时,AP=2,OP=2,OQ=2,PQ=4,PM=PQ=4,
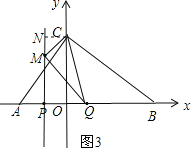
①点M在x轴上方时,如图3,
过点C作CN⊥PM,得:四边形CNPQ是梯形,
∵S△CMQ=S梯形CNPQ﹣S△CNM﹣S△PQM,
∴S△CMQ=![]() (CN+PQ)×PN﹣
(CN+PQ)×PN﹣![]() CNMN﹣
CNMN﹣![]() PMPQ
PMPQ
=![]() ×(OP+PQ)×OC﹣
×(OP+PQ)×OC﹣![]() ×OP×(OC﹣PM)﹣
×OP×(OC﹣PM)﹣![]() ×4×4
×4×4
=![]() ×(2+4)×-
×(2+4)×-![]() ×2×(6﹣4) ﹣8
×2×(6﹣4) ﹣8
=18﹣2﹣8=8;
②点M在x轴下方,如图4.过点C作CN⊥PM,得:四边形CNPQ是梯形,
∵S△CMQ=S梯形CNPQ+S△PQM-S△CNM,
∴S△CMQ=![]() (CN+PQ)PN+
(CN+PQ)PN+![]() PQPM﹣
PQPM﹣![]() MNCN
MNCN
=![]() ×(OP+PQ)×OC+
×(OP+PQ)×OC+![]() ×4×4﹣
×4×4﹣![]() (OC+PM)OP
(OC+PM)OP
=![]() ×(2+4)×6+8﹣
×(2+4)×6+8﹣![]() ×(6+4)×2
×(6+4)×2
=![]() ×6×6+8﹣
×6×6+8﹣![]() ×10×2
×10×2
=18+8﹣10=16.

∴△CMQ的面积为:8或16.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:
【题目】已知正反比例函数的图像交于![]() 、
、![]() 两点,过第二象限的点
两点,过第二象限的点![]() 作
作![]() 轴,点
轴,点![]() 的横坐标为
的横坐标为![]() ,且
,且![]() ,点
,点![]() 在第四象限
在第四象限
(1)求这两个函数解析式;
(2)求这两个函数图像的交点坐标;
(3)若点![]() 在坐标轴上,联结
在坐标轴上,联结![]() 、
、![]() ,写出当
,写出当![]() 时的
时的![]() 点坐标
点坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售面向中考生的计数跳绳,每根成本为20元,销售的前40天内的日销售量m(根)与时间t(天)的关系如表.
时间t(天) | 1 | 3 | 8 | 10 | 26 | … |
日销售量m(件) | 51 | 49 | 44 | 42 | 26 | … |
前20天每天的价格y1(元/件)与时间t(天)的函数关系式为:y1= ![]() t+25(1≤t≤20且t为整数);后20天每天的价格y2(元/件)与时间t(天)的函数关系式为:y2=﹣
t+25(1≤t≤20且t为整数);后20天每天的价格y2(元/件)与时间t(天)的函数关系式为:y2=﹣ ![]() t+40(21≤t≤40且t为整数).
t+40(21≤t≤40且t为整数).
(1)认真分析表中的数据,用所学过的一次函数,二次函数的知识确定一个满足这些数据m(件)与t(天)之间的关系式;
(2)请计算40天中娜一天的日销售利润最大,最大日销售利润是多少?
(3)在实际销售的前20天中,该公司决定每销售一件商品就捐赠a元利润(a<3)给希望工程,公司通过销售记录发现,前20天中扣除捐赠后的日销售利润随时间t(天)的增大而增大,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图所示(1<x=h<2,0<xA<1).下列结论:①2a+b>0;②abc<0; ③若OC=2OA,则2b﹣ac=4; ④3a﹣c<0.其中正确的个数是( ) 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+bx+c的部分图象如图所示,A(1,0),B(0,3).
(1)求抛物线的解析式;
(2)结合函数图象,写出当y<3时x的取值范围. 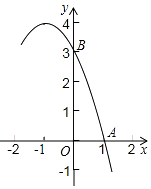
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y=﹣ ![]() x2+mx+m+
x2+mx+m+ ![]() .
.
(1)①无论m取何值,抛物线经过定点P;
②随着m的取值变化,顶点M(x,y)随之变化,y是x的函数,则其函数C2关系式为;
(2)如图1,若该抛物线C1与x轴仅有一个公共点,请在图1中画出顶点M满足的函数C2的大致图象,平行于y轴的直线l分别交C1、C2于点A、B,若△PAB为等腰直角三角形,判断直线l满足的条件,并说明理由;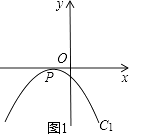
(3)如图2,抛物线C1的顶点M在第二象限,交x轴于另一点C,抛物线上点M与点P之间一点D的横坐标为﹣2,连接PD、CD、CM、DM,若S△PCD=S△MCD , 求二次函数的解析式.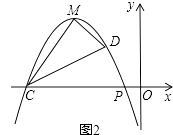
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2ax+c的图象与x轴交于A、B两点(点A在点B的左边)AB=4,与y轴交于点C,OC=OA,点D为抛物线的顶点. 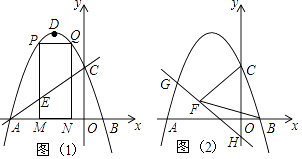
(1)求抛物线的解析式;
(2)点M(m,0)为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N,可得矩形PQNM,如图1,点P在点Q左边,当矩形PQNM的周长最大时,求m的值,并求出此时的△AEM的面积;
(3)已知H(0,﹣1),点G在抛物线上,连HG,直线HG⊥CF,垂足为F,若BF=BC,求点G的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com