
����Ŀ����֪������C1��y=�� ![]() x2+mx+m+
x2+mx+m+ ![]() ��
��
��1��������mȡ��ֵ�������߾�������P��
������m��ȡֵ�仯������M��x��y����֮�仯��y��x�ĺ��������亯��C2��ϵʽΪ��
��2����ͼ1������������C1��x�����һ�������㣬����ͼ1�л�������M����ĺ���C2�Ĵ���ͼ��ƽ����y���ֱ��l�ֱ�C1��C2�ڵ�A��B������PABΪ����ֱ�������Σ��ж�ֱ��l�������������˵�����ɣ�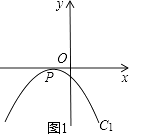
��3����ͼ2��������C1�Ķ���M�ڵڶ����ޣ���x������һ��C���������ϵ�M���P֮��һ��D�ĺ�����Ϊ��2������PD��CD��CM��DM����S��PCD=S��MCD �� ����κ����Ľ���ʽ��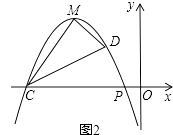
���𰸡�
��1������1��0����y= ![]()
��2��
�⣺�߸�������C1��x�����һ�������㣬
���= ![]() =0��
=0��
m2+2m+1=0��
m1=m2=��1��
��������C1��ϵʽΪ��y=�� ![]() ��x��
��x�� ![]() =��
=�� ![]() ��x+1��2��
��x+1��2��
��ͼ1��������C1��C2����x��Գƣ�
�ߡ�PAB�ǵ���ֱ�������Σ�
��PA=PB��PA��PB��
��x���AB��
��x����AB�Ĵ�ֱƽ���ߣ�
��BD=PD��
��ֱ��l�ڶ���P���Ҳ�ʱ�� ![]() =x+1��
=x+1��
���x=1��x=��1�����ܹ��������Σ���ȥ����
��ֱ��l�ڶ���P�����ʱ���� ![]() =��x��1��
=��x��1��
���x=��3��x=��1�����ܹ��������Σ���ȥ����
��ֱ��lΪ��x=1��x=��3
��3��
�⣺��ͼ2��
��x=��2ʱ��y=�� ![]() ��4��2m+m+
��4��2m+m+ ![]() =��m��
=��m�� ![]() ��
��
��D����2����m�� ![]() ����
����
��y=0ʱ���� ![]() x2+mx+m+
x2+mx+m+ ![]() =0��
=0��
x2��2mx��2m��1=0��
��ã�x1=1��x2=2m+1��
��P����1��0����C��2m+1��0����
�ɣ�1���ã�����M[m�� ![]() ��m+1��2]��
��m+1��2]��
��D��DH��PC��H����M��MN��PC��N����CD��T��
��ֱ��CD�Ľ���ʽΪ��y= ![]() x��m��
x��m�� ![]() ��
��
��T��m���� ![]() ��
�� ![]() ����
����
��S��PCD=S��MCD��
�� ![]() PCDH=
PCDH= ![]() MTCH��
MTCH��
![]() ����1��2m��1������m��
����1��2m��1������m�� ![]() ��=
��= ![]() [
[ ![]() ��
�� ![]() ]����2��2m��1����
]����2��2m��1����
��m+1����2m+3��=�� ![]() ��m+1����m+2����2m+3����
��m+1����m+2����2m+3����
��m+1����2m+3����m+4��=0��
m1=��1��m2=�� ![]() ��m3=��4��
��m3=��4��
��������C1�Ķ���M�ڵڶ����ޣ���D���ڵ�M���P֮�䣬
��m1=��1��m2=�� ![]() �����������⣬��ȥ��
�����������⣬��ȥ��
��m=��4��
��y=�� ![]() x2��4x��4+
x2��4x��4+ ![]() =��
=�� ![]() x2��4x��
x2��4x�� ![]() ��
��
����κ����Ľ���ʽΪ��y=�� ![]() x2��4x��
x2��4x�� ![]() ��
��

���������⣺��1���ٵ�x=��1ʱ��y=�� ![]() ��m+m+
��m+m+ ![]() =0��
=0��
������mȡ��ֵ�������߾�������P����1��0����
y=�� ![]() x2+mx+m+
x2+mx+m+ ![]() =��
=�� ![]() ��x��m��2+
��x��m��2+ ![]() m2+m+
m2+m+ ![]() ��
��
����������m�� ![]() m2+m+
m2+m+ ![]() ����
����
�߶���M��x��y����y��x�ĺ�����
���亯��C2��ϵʽΪ��y= ![]() =
= ![]() ��x+1��2��
��x+1��2��
���Դ��ǣ��٣���1��0������y= ![]() ��
��
�����㾫����������Ĺؼ�����������κ�����ͼ������֪ʶ�����ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣬�Լ��Զ��κ��������ʵ����⣬�˽������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() �ǵȱ������Σ�
�ǵȱ������Σ�![]() ��
��

![]() �����ж�
�����ж�![]() ����״��˵�����ɣ�
����״��˵�����ɣ�
![]() ���
���![]() �Ƶ�
�Ƶ�![]() ��ת������
��ת������![]() �ڵ�
�ڵ�![]() �������ж�
�������ж�![]() ���ܳ��Ƿ����仯��������䣬˵�����ɣ�����仯��˵������
���ܳ��Ƿ����仯��������䣬˵�����ɣ�����仯��˵������![]() ��ʲôλ��ʱ��
��ʲôλ��ʱ��![]() ���ܳ���С��
���ܳ���С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�AB=AC=1����BAC=45�㣬��AEF���ɡ�ABC�Ƶ�A��˳ʱ�뷽����ת�õ��ģ�����BE��CF�ཻ�ڵ�D�� 
��1����֤��BE=CF��
��2�����ı���ACDEΪ����ʱ����BD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�ڣ���OΪ����ԭ�㣬��A��x�Ḻ�����ϣ���B��C�ֱ���x�ᡢy���������ϣ���OB=2OA��OBOC=OCOA=2.
(1)���C�����ꣻ
(2)��P�ӵ�A������ÿ��1����λ���ٶ���AB���B�����˶���ͬʱ��Q�ӵ�B������ÿ��3����λ���ٶ���BA���յ�A�����˶�������Q�����յ�Aʱ����P��Q��ֹͣ�˶������P�˶���ʱ��Ϊt(t��0)�룬�߶�PQ�ij���Ϊy���ú�t��ʽ�ӱ�ʾy����д����Ӧ��t�ķ�Χ��
(3)��(2)�������£�����P��x��Ĵ���PM��PM=PQ���Ƿ����tֵʹ��OΪPQ�е�? ��������tֵ�������ʱ��CMQ�����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ABΪ��O��ֱ������CΪ��Բ��һ�㣬ADƽ�֡�CAB����O�ڵ�D 
��1����֤��OD��AC��
��2����AC=8��AB=10����AD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڼס�������ͬѧ��ѡ��һ�˲μ����л���ʫ��������������ͬ�IJ��������£�����5�β��Գɼ�����λ���֣����£�
�ף�79��86��82��85��83
�ң�88��79��90��81��72��
�ش��������⣺
��1���׳ɼ���ƽ������______ ���ҳɼ���ƽ������______ ��
��2��������֪S��2=6��S��2=42������Ϊѡ��˭�μӱ��������ʣ�˵�����ɣ�
��3������Ӽס�������5�εijɼ��и������ȡһ�γɼ����з�������鵽�������˵ijɼ�������80�ֵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵���д������( )
A. ����ABC�У���C����A����B������ABCΪֱ��������
B. ����ABC�У�����A�á�B�á�C��5��2��3������ABCΪֱ��������
C. ����ABC����a��![]() c��b��
c��b��![]() c������ABCΪֱ��������
c������ABCΪֱ��������
D. ����ABC�У���a��b��c��2��2��4������ABCΪֱ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ӳ��ȷֱ�Ϊ3��5��6��9�������߶�����ȡ����������������εĸ���Ϊ�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڳ�����![]() �ĶԳ���
�ĶԳ���![]() ���ҵ�
���ҵ�![]() ��ʹ��
��ʹ��![]() ��
��![]() ��Ϊ���������Σ������������ĵ�
��Ϊ���������Σ������������ĵ�![]() ��_________��.
��_________��.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com