练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，和是等边三角形，，

    请你判断的形状并说明理由；

    如果绕点旋转，交边于点，请你判断的周长是否发生变化？如果不变，说明理由；如果变化，说明当点在什么位置时，的周长最小．

    【答案】是等边三角形；的周长发生变化，当是中点时的周长最小．

    【解析】

    （1）由∠EDF＝60°，可推得∠EBD＝∠FBC，结合条件可证明△DEB≌△CFB，所以BE＝BF，结合条件可证得△BEF为等边三角形；

    （2）结合（1）可知当BE为AD边上的中线，即点E为AD的中点时其周长最小．

    是等边三角形理由如下：

    ∵和是等边三角形，

    ∴，且，

    ∴

    ∵

    ∴

    在和中，

    ，

    ∴

    ∴

    ∵

    ∴是等边三角形

    的周长发生变化，当是中点时的周长最小．

    因为为等边三角形，所以当最小时周长最小，所以当为边上的中线即当是中点时其周长最小．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】在一次科技活动中，小明进行了模拟雷达扫描实验．如图，表盘是△ABC，其中AB=AC，∠BAC=120°，在点A处有一束红外光线AP，从AB开始，绕点A逆时针匀速旋转，每秒钟旋转15°，到达AC后立即以相同旋转速度返回AB，到达后立即重复上述旋转过程．小明通过实验发现，光线从AB处旋转开始计时，旋转1秒，此时光线AP交BC边于点M，BM的长为（20 ﹣20）cm．
    （1）求AB的长；
    （2）从AB处旋转开始计时，若旋转6秒，此时光线AP与BC边的交点在什么位置？若旋转2014秒，交点又在什么位置？请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】数学活动：探究利用角的对称性构造全等三角形解决问题

    (1)如图①，OP是∠MON的平分线，请你利用该图形画一对以OP所在直线为对称轴的全等三角形；(写出简单做法，不用证明两三角形全等，不用尺规作图亦可）

    (2)如图②，在△ABC中，∠ACB=90°，∠B=60°，AD、CE分别是∠BAC、∠BCA的平分线，AD、CE相交于点F.请直接填空:∠AFE= 度，DF EF(填>，<或=)；

    （3）如图③，在△ABC中，如果∠ACB≠90°，而(2)中的其他条件不变，请问，你在(2)中所得结论是否仍然成立?若成立，请证明；若不成立，请说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知正反比例函数的图像交于、两点，过第二象限的点作轴，点的横坐标为，且，点在第四象限

    （1）求这两个函数解析式；

    （2）求这两个函数图像的交点坐标；

    （3）若点在坐标轴上，联结、，写出当时的点坐标

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的一元二次方程kx2﹣4x+2=0有实数根．
    （1）求k的取值范围；
    （2）若△ABC中，AB=AC=2，AB，BC的长是方程kx2﹣4x+2=0的两根，求BC的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已知，分别为两坐标轴上的点，且，满足，且.

    （1）求、、三点的坐标；

    （2）若，过点的直线分别交、于、两点，且，设、两点的横坐标分别为、，求的值；

    （3）如图2，若，点是轴上点右侧一动点，于点，在上取点，使，连接，当点在点右侧运动时，的度数是否改变?若不变，请求其值；若改变，请说明理由.

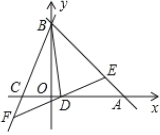
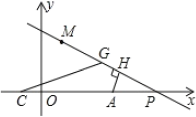
    图1 图2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AD是BC边上的高，AE是∠BAC平分线．

    （1）若∠B=38°，∠C=70°，求∠DAE的度数；

    （2）若∠B＞∠C，试探求∠DAE、∠B、∠C之间的数量关系．

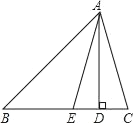
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商店销售面向中考生的计数跳绳，每根成本为20元，销售的前40天内的日销售量m（根）与时间t（天）的关系如表．

    时间t（天）

    1

    3

    8

    10

    26

    …

    日销售量m（件）

    51

    49

    44

    42

    26

    …

    前20天每天的价格y1（元/件）与时间t（天）的函数关系式为：y1= t+25（1≤t≤20且t为整数）；后20天每天的价格y2（元/件）与时间t（天）的函数关系式为：y2=﹣ t+40（21≤t≤40且t为整数）．
    （1）认真分析表中的数据，用所学过的一次函数，二次函数的知识确定一个满足这些数据m（件）与t（天）之间的关系式；
    （2）请计算40天中娜一天的日销售利润最大，最大日销售利润是多少？
    （3）在实际销售的前20天中，该公司决定每销售一件商品就捐赠a元利润（a＜3）给希望工程，公司通过销售记录发现，前20天中扣除捐赠后的日销售利润随时间t（天）的增大而增大，求a的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知抛物线C1：y=﹣ x2+mx+m+ ．
    （1）①无论m取何值，抛物线经过定点P；
    ②随着m的取值变化，顶点M（x，y）随之变化，y是x的函数，则其函数C2关系式为；
    （2）如图1，若该抛物线C1与x轴仅有一个公共点，请在图1中画出顶点M满足的函数C2的大致图象，平行于y轴的直线l分别交C1、C2于点A、B，若△PAB为等腰直角三角形，判断直线l满足的条件，并说明理由；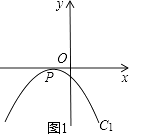

    （3）如图2，抛物线C1的顶点M在第二象限，交x轴于另一点C，抛物线上点M与点P之间一点D的横坐标为﹣2，连接PD、CD、CM、DM，若S△PCD=S△MCD ， 求二次函数的解析式．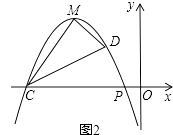

    查看答案和解析>>

    同步练习册答案