
【题目】如图,在 Rt△ABC 中,∠C=90°,AD 平分∠BAC 交 BC 于点 D,O 为 AB 上一点,经过点 A、D 的⊙O 分别交 AB、AC 于点 E、F,
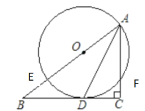
(1)求证:BC 是⊙O 切线;
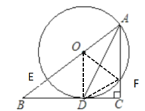
(2)设 AB=m,AF=n,试用含 m、n 的代数式表示线段 AD 的长.
【答案】(1)见解析;(2)![]()
【解析】
(1)连接OD,由AD为角平分线得到∠BAD=∠CAD,再由等边对等角得到∠OAD=∠ODA,等量代换得到∠ODA=∠CAD,进而得到OD∥AC,得到OD与BC垂直,即可得证;
(2)连接DF,由(1)得到BC为圆O的切线,结合角度的运算得出∠CDF=∠DAF,进而得到∠AFD=∠ADB,结合∠BAD=∠DAF得到△ABD∽△ADF,由相似得比例,即可表示出AD;
(1)证明:如图,连接OD,则OD为圆O的半径,
∵AD 平分∠BAC,
∴∠BAD=∠CAD,
∵OD=OA,
∴∠OAD=∠ODA,
∴∠ODA=∠CAD,
∴OD∥AC,
∴∠ODC=∠C=90°
即OD⊥BC,
∴BC 是⊙O 切线.
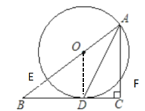
(2)连接DF,OF,由(1)知BC为圆O的切线,
∴∠ODC=90°,
∴∠ODF+∠CDF=90°,
∴∠ODF=90°-∠CDF,
∵OD=OF,
∴∠ODF=∠OFD=![]() ,
,
又∵∠DAF=![]() ,
,
∴∠ODF=![]()
∴∠CDF=∠DAF
又∵∠CDF+∠CFD=90°,∠DAF+∠CDA=90°,
∴∠CDA=∠CFD,
∴∠AFD=∠ADB,
∵∠BAD=∠DAF,
∴△ABD∽△ADF,
∴![]() ,则
,则![]()
∵AB=m,AF=n,
∴![]()
∴![]()


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
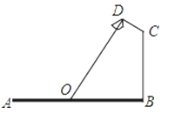
【题目】如图,要在宽为22米的大道两边安装路灯,路灯的灯臂CD长2米,且与灯柱BC成120°角,路灯采用圆锥形灯罩,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线时照明效果最佳,求路灯的灯柱BC高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
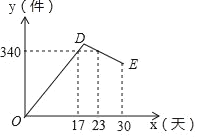
【题目】某公司开发出一款新的节能产品,该产品的成本价为6元件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试营销,售价为9元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少4件,
(1)请直接写出y与x之间的函数关系式;
(2)日销售利润不低于960元的天数共有多少天?试销售期间,日销售最大利润是多少元?
(3)工作人员在统计的过程中发现,有连续两天的销售利润之和为1980元,请你算出是哪两天.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商经销一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下,若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6080元,同时又要顾客得到实惠,那么每千克应涨价多少元?
(2)若该商场单纯从经济角度看,每千克这种水果涨价多少元,能使商场获利最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() (k>0)的图像交于A,B两点,过点A做x轴的垂线,垂足为M,△AOM面积为1.
(k>0)的图像交于A,B两点,过点A做x轴的垂线,垂足为M,△AOM面积为1.
(1)求反比例函数的解析式;
(2)在y轴上求一点P,使PA+PB的值最小,并求出其最小值和P点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
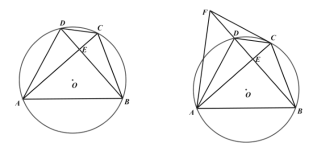
【题目】四边形![]() 是
是![]() 的内接四边形,
的内接四边形,![]() ,
,![]() ,垂足为
,垂足为![]() .
.
(1)如图1,求证:![]() ;
;
(2)如图2,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,连接
,连接![]() 、
、![]() ,求证:
,求证:![]() ;
;
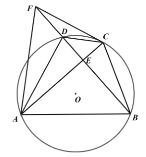
(3)如图3,在(2)的条件下,若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王骑车从甲地到乙地,小李骑车从乙地到甲地,小王的速度小于小李的速度,两人同时出发,沿同一条公路匀速前进.图中的折线表示两人之间的距离![]() 与小王的行驶时间
与小王的行驶时间![]() 之间的函数关系.
之间的函数关系.
请你根据图象进行探究:
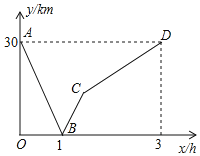
(1)小王和小李的速度分别是多少?
(2)求线段![]() 所表示的
所表示的![]() 与
与![]() 之间的函数解析式,并写出自变量
之间的函数解析式,并写出自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将长方形纸片ABCD折叠,使边DC落在对角线AC上,折痕为CE,且D点落在对角线D′处.若AB=3,AD=4,则ED的长为

A.![]() B.3 C.1 D.
B.3 C.1 D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com