
����Ŀ����ͼ����֪���κ���y= ![]() x2+
x2+ ![]() x��
x�� ![]() ��ͼ����x�ύ�ڵ� A��B���� y ���ڵ� C�������ߵĶ���Ϊ D��
��ͼ����x�ύ�ڵ� A��B���� y ���ڵ� C�������ߵĶ���Ϊ D��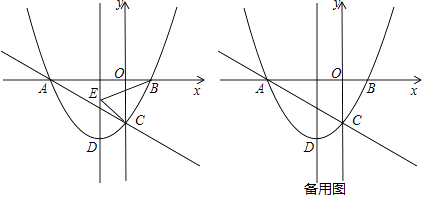
��1���������߶��� D �������Լ�ֱ�� AC �ĺ�������ʽ��
��2���� P ����������һ�㣬�ҵ�P��ֱ�� AC �·����� E �������߶Գ����ϣ�����BCE ���ܳ���Сʱ�����PCE ��������ֵ�Լ���ʱ�� P �����ꣻ
��3���ڣ�2���������£����� P ��ƽ���� AC ��ֱ�߷ֱ�x���ڵ� M���� y ���ڵ�N����������y= ![]() x2+
x2+ ![]() x��
x�� ![]() �ضԳ�������ƽ�ƣ�ƽ�ƺ������ߵĶ���Ϊ D'����ƽ�ƵĹ����У��Ƿ���ڵ� D'��ʹ�õ� D'��M��N ���㹹�ɵ�������Ϊֱ�������Σ������ڣ�ֱ��д���� D'�����ꣻ�������ڣ���˵�����ɣ�
�ضԳ�������ƽ�ƣ�ƽ�ƺ������ߵĶ���Ϊ D'����ƽ�ƵĹ����У��Ƿ���ڵ� D'��ʹ�õ� D'��M��N ���㹹�ɵ�������Ϊֱ�������Σ������ڣ�ֱ��д���� D'�����ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1���⣺y= ![]() x2+
x2+ ![]() x��
x�� ![]() =
= ![]() ��x+1��2��
��x+1��2�� ![]() ������D����������1����
������D����������1���� ![]() ����
����
��y=0ʱ�� ![]() x2+
x2+ ![]() x��
x�� ![]() =0�����x1=��3��x2=1��
=0�����x1=��3��x2=1��
��A����3��0����B��1��0����
��x=0ʱ��y=�� ![]() ��
��
��C��0���� ![]() ����
����
��ֱ��AC�Ľ���ʽΪy=�� ![]() x��
x�� ![]()
��2���⣺�ߡ�CPE���ܳ�ΪBC+CE+BE������BC�ij��ǹ̶��ģ�
���ܳ�ȡ����Сֵ����BE+CEȡ����Сֵ��
�ߵ�E�������߶Գ�����һ�㣬
��BE=AE��
��BE+CE=AE+CE��
��BE+CE����Сֵ��AC����E��AC��Գ���Ľ��㣮
���E����1���� ![]() ����
����
�ߵ�P����������x���·�һ�㣬���PΪ��t�� ![]() t2+
t2+ ![]() t��
t�� ![]() ������
������ ![]() t2+
t2+ ![]() t��
t�� ![]() ��0��
��0��
����P��QP��x�ύֱ��AC�ڵ�Q����Q����Ϊ��t���� ![]() t��
t�� ![]() ����
����
����p�ڶԳ������ʱ��S��PCE=S��PCQ��S��PEQ= ![]() PQ��0��t����
PQ��0��t���� ![]() PQ����1��t��=
PQ����1��t��= ![]() PQ��
PQ��
����P�ڶԳ�����Ҳ�ʱ��S��PCE=S��PCQ+S��PEQ= ![]() PQ��0��t��+
PQ��0��t��+ ![]() PQ[t������1��]=
PQ[t������1��]= ![]() PQ��
PQ��
��PQ=���� ![]() t��
t�� ![]() ������
������ ![]() t2+
t2+ ![]() t��
t�� ![]() ��=��
��=�� ![]() t2��
t2�� ![]() t��
t��
��S��PCE= ![]() PQ=��
PQ=�� ![]() t2��
t2�� ![]() t=��
t=�� ![]() ��t+
��t+ ![]() ��2+
��2+ ![]() ��
��
��t=�� ![]() ʱ����PEC�����������ֵ��
ʱ����PEC�����������ֵ�� ![]() ����ʱ����P������Ϊ����
����ʱ����P������Ϊ���� ![]() ����
���� ![]() ��
��
��3���⣺������P��ƽ����AC��ֱ��MN�Ľ���ʽΪy=�� ![]() x��
x�� ![]() ��
��
��x=0ʱ��y=�� ![]() ����N��0����
����N��0���� ![]() ������y=0ʱ��x=��
������y=0ʱ��x=�� ![]() ����M����
����M���� ![]() ��0����
��0����
���D�����������1��d������MN2=���� ![]() ��2+����
��2+���� ![]() ��2=
��2= ![]() ��MD��2=[��
��MD��2=[�� ![]() ������1��]2+d2=
������1��]2+d2= ![]() +d2��ND��2=����1��2+����
+d2��ND��2=����1��2+���� ![]() ��d��2=d2+
��d��2=d2+ ![]() d+
d+ ![]() ��
��
����MD��N=90��ʱ��MD��2+ND��2=MN2���� ![]() +d2+d2+
+d2+d2+ ![]() d+
d+ ![]() =
= ![]() ��
��
��������4d2+7 ![]() d��17=0�����d1=
d��17=0�����d1= ![]() ��d2=
��d2= ![]() ��
��
����NMD��=90��ʱ��MD��2=ND��2+MN2���� ![]() +d2=d2+
+d2=d2+ ![]() d+
d+ ![]() +
+ ![]() ��
��
���� ![]() d=��
d=�� ![]() �����d=��
�����d=�� ![]() ��
��
����NMD�䩁90��ʱ��ND��2=MD��2+MN2����d2+ ![]() d+
d+ ![]() =
= ![]() +d2+
+d2+ ![]() ��
��
���� ![]() d=
d= ![]() �����d=
�����d= ![]() ��
��
����ڵ� D'��ʹ�õ� D'��M��N ���㹹�ɵ�������Ϊֱ�������Σ�D��������Ϊ����1�� ![]() ������1��
������1�� ![]() ��������1��
��������1�� ![]() ������1
������1 ![]() ��
��
����������1�������䷽������ɶ���ʽ������������ꣻ��2����BCE ���ܳ���С����CE+BE��С���ɶԳƷ�����õ�E��AC��Գ���Ľ��㴦ʱ����BCE ���ܳ���С����PCE ��������ֵ�����ú���˼�룬���P�ĺ�����Ϊt������������t�Ĵ���ʽ��ʾ������x�ᴹ�ߣ��ѡ�PCE �ָ�Ϊ��������ֱ�ߵ������Σ�������������ĺ�������ɶ���ʽ�����ֵ����3��D'��M��N ���㹹�ɵ�������Ϊֱ����������������ۣ���MD��N=90����NMD��=90����NMD�䩁90�㣬���ù��ɶ����г�����.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����������ϣ��ش����⣬����һ������ֱ��y��ax+b��ֱ��y��bx+a��Ϊ����ͬ��ֱ�ߡ������磬ֱ��y��x+4��ֱ��y��4x+l��Ϊ����ͬ��ֱ�ߡ���
���϶������ڰ���ֱ������ϵ�е���������P1��x1��y1����P2��x2��y2����P1��P2֮������ֱ�Ǿ���d1��P1��p2����|x1��x2|+|y1��y2|�����磺Q1����3��1����Q2��2.4��������ֱ�Ǿ���Ϊd��Q1��Q2����|��3��2|+|1��4|��8�� P0��x0��y0��Ϊһ�����㣬Q��x��y����ֱ��y��ax+b�ϵĶ��㣬���ǰ�d��P0��Q������Сֵ����Po��ֱ��y��ax+b��ֱ�Ǿ��룮
��1������S����2��6����T��1��3��������ֱ�Ǿ���d��S��T������ ����ֱ��y��4x+3�ϵ�һ��H��a��b���������ġ���ͬ��ֱ�ߡ��ϵĵ㣬���H�����꣮
��2������ֱ��y��ax+b�ϵ�����һ��M��m��n�������е�N��3m��2m��3n�������ġ���ͬ��ֱ�ߡ��ϣ������L��10����![]() ����ֱ��y��ax+b��ֱ�Ǿ��룮
����ֱ��y��ax+b��ֱ�Ǿ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�E��AD���е㣬�ӳ�CE��BA���ڵ�F������AC��DF��
��1����֤���ı���ACDF��ƽ���ı��Σ�
��2����CFƽ�֡�BCDʱ��д��BC��CD��������ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ů��������������̤�࣬ij��Ʒ��Ьר����ץס����������10�����������г�����M���˶�Ь���д�����M���˶�Ьÿ˫�ijɱ���Ϊ800Ԫ�����Ϊ1200Ԫ��
��1��M���˶�Ьÿ˫��ཱུ�۶���Ԫ������ʹ�����ʲ�����20%��
��2���õ���ǰÿ�ܹ��۳�M���˶�Ь100˫��2017��3�µ�һ����ĩ��ǡ���Ǹõ��10������죬�����ĩM���˶�Ьÿ˫�ڱ�۵Ļ����Ͻ��� ![]() m%����������ĩ������M���˶�Ь��������ԭ��һ��������M���˶�Ь������������
m%����������ĩ������M���˶�Ь��������ԭ��һ��������M���˶�Ь������������ ![]() m%��������ĩ������ﵽ��40000Ԫ����m��ֵ��
m%��������ĩ������ﵽ��40000Ԫ����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������������ÿ̨���۷ֱ�Ϊ2000Ԫ��1700Ԫ��![]() ��
��![]() �����ͺŵĿյ�������ǽ����ܵ����������
�����ͺŵĿյ�������ǽ����ܵ����������
����ʱ�� | �������� | ���ۿ� | |
|
| ||
��һ�� | 4̨ | 5̨ | 20500Ԫ |
�ڶ��� | 5̨ | 10̨ | 33500Ԫ |
��1����![]() ��
��![]() �����ͺŵĿյ������۵��ۣ�
�����ͺŵĿյ������۵��ۣ�
��2��������ܵ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���������ֱ��A��B���س���������������ʻ����֪�ҳ��ȳ�����1Сʱ��׳��ٳ�����һ��ʱ�������������ϢվC������������C�غ��ҳ�����Ϣ������ԭ��ǰ��A�أ��׳���Ϣ��Сʱ���ٰ�ԭ��ǰ��B�أ��׳�����B��ֹͣ�˶����ҳ���A�غ�����ԭ�ٷ���B�أ���֪������ľ���y��km�����ҳ��˶���ʱ��x��h���仯��ͼ���׳�����B��ʱ���ҳ�����B�صľ���Ϊ_____��km����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������������ѧ�Ļ���������Ϊ�˽�һ���˽�ѧ���ļ����������2020����ѧ��ʦ�Ƕ�ij�ο����е�19�������ĵ÷���������˵��飬�ֱַ��A��B�����������ȡ10��ѧ���ijɼ����£�
A��10��ѧ���ijɼ����������ͳ��ͼ������ͼ��

B��10��ѧ���ijɼ�����λ���֣��ֱ�Ϊ��9��8��9��10��9��7��9��8��10��8
������ʦ������ȡѧ���ɼ���������������õ������±����ݣ�
A�� | B�� | |
ƽ���� | 8.3 | a |
��� | b | 9 |
���� | 8��10 | c |
���� | 4 | 3 |
���� | 1.81 | 0.81 |
����������Ϣ������������⣮
��1����ȫ����ͳ��ͼ��
��2��ֱ��д������a��b��c��ֵ��a���� ����b���� ����c���� ����
��3�������������ݣ�����ΪA��B�������ĸ�����������յø��ã���˵�����ɣ�д�������������ɣ����� ����
��4����9�ּ�9������Ϊ���㣬��A�55�ˣ���A�����������Ĵ�Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l��y=kx��������C��y=ax2+bx+1��
����k=1��b=1ʱ��������C��y=ax2+bx+1�Ķ�����ֱ��l��y=kx�ϣ���a��ֵ��
��������ֱ��l����ƽ��k2+1����λ���ȵõ�ֱ��r�������۷���ʵ��kȡ��ֵ��ֱ��r��������C��ֻ��һ�����㣻
��i����������ߵĽ���ʽ��
��ii����P�Ǵ�����������һ�㣬����P��PQ��y������ֱ��y=2���ڵ�Q��OΪԭ�㣬��֤��OP=PQ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
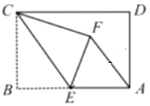
����Ŀ������ABCD�У�AB=4��BC=3����EΪAB���е㣬������ABCD��CE�۵���ʹ�õ�B�䵽��F��λ��.
(1)��֤��AF��CE.
(2)��AF�ij���.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com