
【题目】已知直线l:y=kx和抛物线C:y=ax2+bx+1.
(Ⅰ)当k=1,b=1时,抛物线C:y=ax2+bx+1的顶点在直线l:y=kx上,求a的值;
(Ⅱ)若把直线l向上平移k2+1个单位长度得到直线r,则无论非零实数k取何值,直线r与抛物线C都只有一个交点;
(i)求此抛物线的解析式;
(ii)若P是此抛物线上任一点,过点P作PQ∥y轴且与直线y=2交于点Q,O为原点,求证:OP=PQ.
【答案】解:(Ⅰ)将k=1,b=1代入代入得:抛物线的解析式为y=ax2+x+1,直线的解析式为y=x.
∵y=ax2+x+1=a(x+ ![]() )2+1﹣
)2+1﹣ ![]() ,
,
∴抛物线的顶点为(﹣ ![]() ,1﹣
,1﹣ ![]() ).
).
∵抛物线的顶点在直线y=x上,
∴﹣ ![]() =1﹣
=1﹣ ![]() ,解得:a=﹣
,解得:a=﹣ ![]() .
.
(Ⅱ)(i)将直线y=kx向上平移k2+1个单位,所得直线的解析式为y=kx+k2+1.
∵无论非零实数k取何值,直线与抛物线都只有一个交点,
∴方程kx+k2+1=ax2+bx+1有两个相等的实数根,即ax2+(b﹣k)x﹣k2=0有两个相等的实数根,
∴△=(b﹣k)2+4ak2=(4a+1)k2﹣2bk+b2=0.
∵无论非零实数k取何值时,(4a+1)k2﹣2bk+b2=0恒成立,
∴4a+1=0且b=0,
∴a=﹣ ![]() ,b=0.
,b=0.
∴抛物线的解析式为y=﹣ ![]() x2+1.
x2+1.
(ii)证明:根据题意,画出图象如图所示:
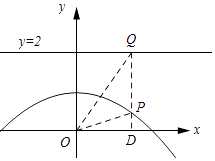
设点P的坐标为(x,﹣ ![]() x2+1)则点Q的坐标为(x,2),D(x,0).
x2+1)则点Q的坐标为(x,2),D(x,0).
∴PD=|﹣ ![]() x2+1|,OD=|x|,QP=2﹣(﹣
x2+1|,OD=|x|,QP=2﹣(﹣ ![]() x2+1)=
x2+1)= ![]() x2+1.
x2+1.
在Rt△OPD中,依据勾股定理得:OP= ![]() =
= ![]() =
= ![]() x2+1.
x2+1.
∴OP=PQ
【解析】(1)利用配方法求出顶点坐标,代入y=x中即可;(2)可联立直线和抛物线解析式得到的方程判别式恒等于0,可得出a、b的值;(3)可表示出OP,PQ,证得二者相等.
【考点精析】本题主要考查了二次函数的图象的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点才能正确解答此题.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA中点,点P在BC上以每秒1个单位的速度由C向B运动,设运动时间为t秒.

(1)△ODP的面积S=________.
(2)t为何值时,四边形PODB是平行四边形?
(3)在线段PB上是否存在一点Q,使得ODQP为菱形?若存在,求t的值,并求出Q点的坐标;若不存在,请说明理由;
(4)若△OPD为等腰三角形,请写出所有满足条件的点P的坐标(请直接写出答案,不必写过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y= ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() 的图象与x轴交于点 A,B,交 y 轴于点 C,抛物线的顶点为 D.
的图象与x轴交于点 A,B,交 y 轴于点 C,抛物线的顶点为 D.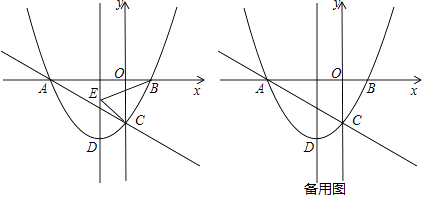
(1)求抛物线顶点 D 的坐标以及直线 AC 的函数表达式;
(2)点 P 是抛物线上一点,且点P在直线 AC 下方,点 E 在抛物线对称轴上,当△BCE 的周长最小时,求△PCE 面积的最大值以及此时点 P 的坐标;
(3)在(2)的条件下,过点 P 且平行于 AC 的直线分别交x轴于点 M,交 y 轴于点N,把抛物线y= ![]() x2+
x2+ ![]() x﹣
x﹣ ![]() 沿对称轴上下平移,平移后抛物线的顶点为 D',在平移的过程中,是否存在点 D',使得点 D',M,N 三点构成的三角形为直角三角形,若存在,直接写出点 D'的坐标;若不存在,请说明理由.
沿对称轴上下平移,平移后抛物线的顶点为 D',在平移的过程中,是否存在点 D',使得点 D',M,N 三点构成的三角形为直角三角形,若存在,直接写出点 D'的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆不仅是网红城市,更是拥有长安,力帆等大型车企的一座汽车城,为了更好的推广和销售汽车,每年都会在悦来会展中心举办大型车展.去年该车展期间大众旗下两品牌汽车迈腾和途观L共计销售240辆,迈腾销售均价为每辆20万元,途观L销售均价为每辆30万元,两种车型去年车展期间销售额共计5600万元.
(1)这两种车型在去年车展期间各销售了多少辆?
(2)在今年的该车展上,各大汽车经销商纷纷采取降价促销手段,而途观L坚持不降价,与去年相比,销售均价不变,销量比去年车展期间减少了a%,而迈腾销售均价比去年降低了a%,销量较去年增加了2a%,两种车型今年车展期间销售总额与去年相同,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=3,AC=4,BC=5,P 为边 BC 上一动点,PE⊥AB 于 E,PF⊥AC于 F,M 为 EF 中点,则 AM 的最小值为( )

A.1B.1.3C.1.2D.1.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把△ABC绕点A按逆时针方向旋转θ度,并使各边长变为原来的n倍,得到△AB′C′,即如图,∠BAB′=θ, ![]() =
= ![]() =
= ![]() =n,我们将这种变换记为[θ,n].△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,那么θ= , n= .
=n,我们将这种变换记为[θ,n].△ABC中,AB=AC,∠BAC=36°,BC=1,对△ABC作变换[θ,n]得△AB′C′,使点B、C、B′在同一直线上,且四边形ABB′C′为平行四边形,那么θ= , n= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,对角线
中,对角线![]() ,
,![]() 相较于点
相较于点![]() ,以
,以![]() 为边向外作等边
为边向外作等边![]() ,连接
,连接![]() ,交
,交![]() 于
于![]() .
.
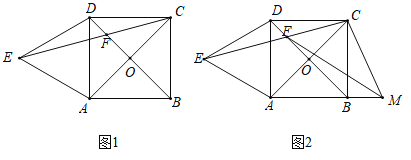
(1)如图1,若![]() ,求
,求![]() 的长
的长
(2)如图2,点![]() 为
为![]() 的延长线上一点,连接
的延长线上一点,连接![]() ,连接
,连接![]() 且
且![]() 平分
平分![]() .求证:
.求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,设坐标轴的单位长度为1cm,整数点P从原点O出发,速度为1cm/s,且点P只能向上或向右运动,请回答下列问题:
(1)填表:

(2)当P点从点O出发10秒,可得到的整数点的个数是 个.
(3)当P点从点O出发 秒时,可得到整数点(10 ,5).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com