
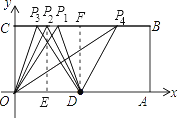
����Ŀ����֪����ͼ��OΪ����ԭ�����ı���OABCΪ������A��10��0����C��0��4������D��OA�е�����P��BC����ÿ��1����λ���ٶ���C��B�˶������˶�ʱ��Ϊt�룮

��1����ODP�����S=________��
��2��tΪ��ֵʱ���ı���PODB��ƽ���ı��Σ�
��3�����߶�PB���Ƿ����һ��Q��ʹ��ODQPΪ���Σ�����������t��ֵ�������Q���������������������˵��������
��4������OPDΪ��������������д���������������ĵ�P�����꣨��ֱ��д����������д���̣�
���𰸡���1��10����2��5����3����8��4������4�����������ĵ�P������ΪP1��3��4����P2��2.5��4����P3��2��4����P4��8��4��.
��������
������1�����������ε������ʽ���������ODP�����S��
��2������PB��OD������ƽ���ı��ε��ж���֪��PB=OD=5ʱ���ı���PODB��ƽ���ı��Σ������PC=5���Ӷ����t��ֵ��
��3���������ε��ж�����OD=OP=PQ=5ʱ���ı���ODQPΪ���Σ���Rt��OPC�У����ù��ɶ������CP��ֵ���������t��ֵ��Q������ꣻ
��4������OPDΪ����������ʱ������������������ۣ������OΪ���㣬��ôOP=OD=5�������PΪ���㣬��ôPO=PD�������DΪ���㣬��ôDP=DO=5���ֱ��������ߣ����ù��ɶ������P�������.
�����������1����OΪ����ԭ�㣬A��10��0�����ı���OABCΪ���Σ�C��0��4����
��OA=BC=10��OC=4��
����D��OA�е㣬
��OD=DA= ![]() OA=5��
OA=5��
���ODP�����S= ![]() ODOC=
ODOC= ![]() ��5��4=10��
��5��4=10��
��2���⣺��PB��OD��
�൱PB=ODʱ���ı���PODB��ƽ���ı��Σ�
��OD=5��
��PB=5��
��PC=BC��PB=10��5=5��
�ߵ�P��BC����ÿ��1����λ���ٶ���C��B�˶���
��t=5
��3���⣺��OD=OP=PQ=5ʱ��ODQPΪ���Σ�
��Rt��OPC�У��ɹ��ɶ����ã�
PC= ![]() =
= ![]() =3��
=3��
��t=3��CQ=CP+PQ=3+5=8��
��Q���������8��4��
��4���⣺��OPDΪ����������ʱ�������������
�����OΪ���㣬��ôOP=OD=5��
�ɹ��ɶ����������PC=3����ʱP1��3��4����
�����PΪ���㣬��ôPO=PD��
��PE��OA��E����OE=ED=2.5����ʱP2��2.5��4����
�����DΪ���㣬��ôDP=DO=5��
��DF��BC��F���ɹ��ɶ�������PF=3��
��P3C=5��3=2��P4C=5+3=8����ʱP3��2��4����P4��8��4����
�������������������ĵ�P������ΪP1��3��4����P2��2.5��4����P3��2��4����P4��8��4����


 ��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������Ѿ��벻�����룬��ȡ������ȶ���Ҫ���룬��һ���á���ʽ�ֽ⡱�����������룬������䣮ԭ���ǣ�����ڶ���ʽ![]() ����ʽ�ֽ�Ľ����
����ʽ�ֽ�Ľ����![]() ����ȡ
����ȡ![]() ��
��![]() ʱ�������ʽ��ֵ�ǣ�
ʱ�������ʽ��ֵ�ǣ�![]() ��
��![]() ��
��![]() ������Щֵ��С�������еõ�
������Щֵ��С�������еõ�![]() �����ǾͿ��ѡ�018162����Ϊһ����λ�������룮���ڶ���ʽ
�����ǾͿ��ѡ�018162����Ϊһ����λ�������룮���ڶ���ʽ![]() ��ȡ
��ȡ![]() ��
��![]() ʱ������д����������������������_________��
ʱ������д����������������������_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�����������ϣ��ش����⣬����һ������ֱ��y��ax+b��ֱ��y��bx+a��Ϊ����ͬ��ֱ�ߡ������磬ֱ��y��x+4��ֱ��y��4x+l��Ϊ����ͬ��ֱ�ߡ���
���϶������ڰ���ֱ������ϵ�е���������P1��x1��y1����P2��x2��y2����P1��P2֮������ֱ�Ǿ���d1��P1��p2����|x1��x2|+|y1��y2|�����磺Q1����3��1����Q2��2.4��������ֱ�Ǿ���Ϊd��Q1��Q2����|��3��2|+|1��4|��8�� P0��x0��y0��Ϊһ�����㣬Q��x��y����ֱ��y��ax+b�ϵĶ��㣬���ǰ�d��P0��Q������Сֵ����Po��ֱ��y��ax+b��ֱ�Ǿ��룮
��1������S����2��6����T��1��3��������ֱ�Ǿ���d��S��T������ ����ֱ��y��4x+3�ϵ�һ��H��a��b���������ġ���ͬ��ֱ�ߡ��ϵĵ㣬���H�����꣮
��2������ֱ��y��ax+b�ϵ�����һ��M��m��n�������е�N��3m��2m��3n�������ġ���ͬ��ֱ�ߡ��ϣ������L��10����![]() ����ֱ��y��ax+b��ֱ�Ǿ��룮
����ֱ��y��ax+b��ֱ�Ǿ��룮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ں��ݴ������������������еĹ����У��ŻԺ����������μ�־Ը�����ʱ�������ĸ�־Ը�߹�����λ������ѡ���������λ��������̳�������ǣ�����¥������ֱ��� ![]() ��ʾ����
��ʾ����
���������λ����������֪ʶ��������ͨ��ȫ֪ʶ�������ֱ��� ![]() ��ʾ����
��ʾ����
��1���Ż�ͬѧ���ĸ���λ�����ѡȡһ��������ǡ��ѡ���������λ����Ϊ����
��2�����ŻԺ�������������ĸ���λ��ѡһ������������������״ͼ���б����������ǡ�ö�ѡ��ͬһ����λ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ��ڽ���ƽ��ֱ������ϵ����ABC�Ķ�����ڸ���ϣ���C������Ϊ��4����1����

��1����������ABC��CΪ��ת���ģ���˳ʱ�뷽����ת90�����ͼ����A1B1C��
��2����ԭ��OΪ�Գ����ģ��ٻ�������ABC����ԭ��O�ԳƵ���A2B2C2����д����C2�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������㹻��ĺڰ�Χ���ӣ��ڳ�һ�����С��֣�����ͼ���У��ڢٸ�ͼ������4 ö���Ӻ�4ö���ӣ��ڢڸ�ͼ������6ö���Ӻ�11ö���ӣ��ڢ۸�ͼ������8ö���Ӻ�18ö���ӣ��������˹������У���ڢ��ͼ���к��ӺͰ��ӵ�ö���ֱ�Ϊ�� ��
A.14��48
B.16��48
C.18��53
D.18��67
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�E��AD���е㣬�ӳ�CE��BA���ڵ�F������AC��DF��
��1����֤���ı���ACDF��ƽ���ı��Σ�
��2����CFƽ�֡�BCDʱ��д��BC��CD��������ϵ����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ů��������������̤�࣬ij��Ʒ��Ьר����ץס����������10�����������г�����M���˶�Ь���д�����M���˶�Ьÿ˫�ijɱ���Ϊ800Ԫ�����Ϊ1200Ԫ��
��1��M���˶�Ьÿ˫��ཱུ�۶���Ԫ������ʹ�����ʲ�����20%��
��2���õ���ǰÿ�ܹ��۳�M���˶�Ь100˫��2017��3�µ�һ����ĩ��ǡ���Ǹõ��10������죬�����ĩM���˶�Ьÿ˫�ڱ�۵Ļ����Ͻ��� ![]() m%����������ĩ������M���˶�Ь��������ԭ��һ��������M���˶�Ь������������
m%����������ĩ������M���˶�Ь��������ԭ��һ��������M���˶�Ь������������ ![]() m%��������ĩ������ﵽ��40000Ԫ����m��ֵ��
m%��������ĩ������ﵽ��40000Ԫ����m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l��y=kx��������C��y=ax2+bx+1��
����k=1��b=1ʱ��������C��y=ax2+bx+1�Ķ�����ֱ��l��y=kx�ϣ���a��ֵ��
��������ֱ��l����ƽ��k2+1����λ���ȵõ�ֱ��r�������۷���ʵ��kȡ��ֵ��ֱ��r��������C��ֻ��һ�����㣻
��i����������ߵĽ���ʽ��
��ii����P�Ǵ�����������һ�㣬����P��PQ��y������ֱ��y=2���ڵ�Q��OΪԭ�㣬��֤��OP=PQ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com