
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+1交y轴于点A,交x轴正半轴于点B(4,0),与过A点的直线相交于另一点D(3,![]() ),过点D作DC⊥x轴,垂足为C.
),过点D作DC⊥x轴,垂足为C.
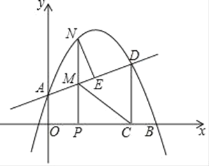
(1)求抛物线的表达式;
(2)点P在线段OC上(不与点O,C重合),过P作PN⊥x轴,交直线AD于M,交抛物线于点N,NE⊥AD于点E,求NE的最大值;
(3)若P是x轴正半轴上的一动点,设OP的长为t.是否存在t,使以点M,C,D,N为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,请说明理由.
【答案】(1)y=﹣![]() x2+
x2+![]() x+1;(2)
x+1;(2)![]() ;(3)t=
;(3)t=![]() 时,以点M,C,D,N为顶点的四边形是平行四边形
时,以点M,C,D,N为顶点的四边形是平行四边形
【解析】
(1)把B(4,0),点D(3,![]() )代入y=ax2+bx+1即可得出抛物线的解析式;
)代入y=ax2+bx+1即可得出抛物线的解析式;
(2)先用含t的代数式表示P、M坐标,再根据三角形的面积公式求出△PCM的面积与t的函数关系式,然后运用配方法可求出△PCM面积的最大值;
(3)若四边形DCMN为平行四边形,则有MN=DC,故可得出关于t的二元一次方程,解方程即可得到结论.
(1)将点B、D的坐标代入二次函数表达式得:
 ,解得:
,解得: ,
,
则函数的表达式为:y=﹣![]() x2+
x2+![]() x+1;
x+1;
(2)设直线AD函数表达式为:y=mx+n,将点A(0,1)、D (3,![]() )代入得:
)代入得:
 解得:
解得:
∴直线AD的表达式为:y=![]() x+1,
x+1,
∴A点的坐标为(0,1)
设直线AD 与x轴交于H点,则H(-2,0)
∴tan∠AHO=![]() ,
,
∵PN⊥x轴, NE⊥AD
则tan∠ENP=an∠AHO=![]() ,则cos∠ENP=
,则cos∠ENP=![]() ,
,
设点N(m,﹣![]() m2+
m2+![]() m+1)、点M(
m+1)、点M(![]() m+1),
m+1),
则NE=MNcos∠ENP=![]() (﹣
(﹣![]() m2+
m2+![]() m+1﹣
m+1﹣![]() m﹣1)=﹣
m﹣1)=﹣![]() (m﹣
(m﹣![]() )2+
)2+![]() ,
,
故当m=![]() 时,则NE的最大值为
时,则NE的最大值为![]() ;
;

(3)设:OP=t,则点M(t,![]() t+1)、N(t,﹣
t+1)、N(t,﹣![]() t2+
t2+![]() t+1),
t+1),
∴|MN|=|-![]() t2+
t2+![]() t+1-
t+1-![]() t-1|=|-
t-1|=|-![]() t2+
t2+![]() t|,CD=
t|,CD=![]() ,
,
如图1,如果以点M、C、D、N为顶点的四边形是平行四边形,

∴MN=CD,即-![]() t2+
t2+![]() t=
t=![]() ,整理得:3t2-9t+10=0,
,整理得:3t2-9t+10=0,
∵△=-39,
∴方程无实数根,
∴此种情况不存在t,
如图2,如果以点M、C、D、N为顶点的四边形是平行四边形,

∴MN=CD,即![]() t2-
t2-![]() t=
t=![]() ,
,
∴t=![]() 或
或![]() (负值舍去),
(负值舍去),
∴当t=![]() 时,以点M、C、D、N为顶点的四边形是平行四边形.
时,以点M、C、D、N为顶点的四边形是平行四边形.


科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(1,4),B(4,n)两点.
的图象交于A(1,4),B(4,n)两点.
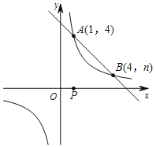
(1)求反比例函数和一次函数的解析式;
(2)直接写出当x>0时,![]() 的解集.
的解集.
(3)点P是x轴上的一动点,试确定点P并求出它的坐标,使PA+PB最小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC,BD相交于点O,延长AC到E,使CE=CO,连接EB,ED.
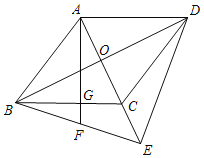
(1)求证:EB=ED;
(2)过点A作AF⊥AD,交BC于点G,交BE于点F,若∠AEB=45°,
①试判断△ABF的形状,并加以证明;
②设CE=m,求EF的长(用含m的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,∠B=90°,
中,∠B=90°,![]() ,点D,E分别是边BC,AC的中点,连接
,点D,E分别是边BC,AC的中点,连接![]() 将
将![]() 绕点C按顺时针方向旋转,记旋转角为
绕点C按顺时针方向旋转,记旋转角为![]() .
.
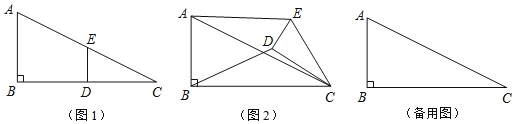
![]() 问题发现:
问题发现:
![]() 当
当![]() 时,
时,![]() _____;
_____;![]() 当
当![]() 时,
时,![]() _____.
_____.
![]() 拓展探究:
拓展探究:
试判断:当![]() 时,
时,![]() 的大小有无变化?请仅就图2的情况给出证明.
的大小有无变化?请仅就图2的情况给出证明.
![]() 问题解决:
问题解决:
当![]() 旋转至A、D、E三点共线时,直接写出线段BD的长.
旋转至A、D、E三点共线时,直接写出线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
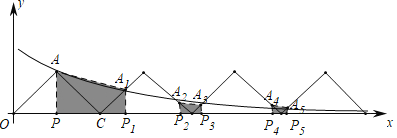
【题目】如图,在△AOC中,∠OAC=90°,AO=AC,OC=2,将△AOC放置于平面直角坐标系中,点O与坐标原点重合,斜边OC在x轴上.反比例函数y=![]() (x>0)的图象经过点A.将△AOC沿x轴向右平移2个单位长度,记平移后三角形的边与反比例函数图象的交点为A1,A2.重复平移操作,依次记交点为A3,A4,A5,A6…分别过点A,A1,A2,A3,A4,A5…作x轴的垂线,垂足依次记为P,P1,P2,P3,P4,P5…若四边形APP1A1的面积记为S1,四边形A2P2P3A3的面积记为S2…,则Sn=_____.(用含n的代数式表示,n为正整数)
(x>0)的图象经过点A.将△AOC沿x轴向右平移2个单位长度,记平移后三角形的边与反比例函数图象的交点为A1,A2.重复平移操作,依次记交点为A3,A4,A5,A6…分别过点A,A1,A2,A3,A4,A5…作x轴的垂线,垂足依次记为P,P1,P2,P3,P4,P5…若四边形APP1A1的面积记为S1,四边形A2P2P3A3的面积记为S2…,则Sn=_____.(用含n的代数式表示,n为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知锐角![]() 内接于⊙O,
内接于⊙O, ![]() 于点D,连结AO.
于点D,连结AO.
⑴若![]() .
.
①求证:![]() ;
;
②当![]() 时,求
时,求![]() 面积的最大值;
面积的最大值;
⑵点E在线段OA上,![]() ,连接DE,设
,连接DE,设![]() ,
,![]() (m、n是正数),若
(m、n是正数),若![]() ,求证:
,求证:![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
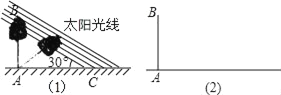
【题目】某数学兴趣小组,利用树影测量树高,如图(1),已测出树AB的影长AC为12米,并测出此时太阳光线与地面成30°夹角.
(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变.求树的最大影长.(用图(2)解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=﹣x2+2tx+2.
(1)求抛物线的对称轴(用含t的代数式表示);
(2)将点A(﹣1,3)向右平移5个单位长度,得到点B.
①若抛物线经过点B求t的值;
②若抛物线与线段AB恰有一个交点,结合函数图象直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
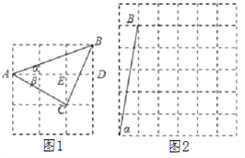
【题目】(1)如图1,如果ɑ,β都为锐角,且tanɑ=![]() ,tanβ=
,tanβ=![]() ,则ɑ+β=___________;
,则ɑ+β=___________;
(2)如果ɑ,β都为锐角,当tanɑ=5,tanβ=![]() 时,在图2的正方形网格中,利用已作出的锐角ɑ,画出∠MON,使得∠MON=ɑ-β.此时ɑ-β=__________度.
时,在图2的正方形网格中,利用已作出的锐角ɑ,画出∠MON,使得∠MON=ɑ-β.此时ɑ-β=__________度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com