
【题目】如图,已知锐角![]() 内接于⊙O,
内接于⊙O, ![]() 于点D,连结AO.
于点D,连结AO.
⑴若![]() .
.
①求证:![]() ;
;
②当![]() 时,求
时,求![]() 面积的最大值;
面积的最大值;
⑵点E在线段OA上,![]() ,连接DE,设
,连接DE,设![]() ,
,![]() (m、n是正数),若
(m、n是正数),若![]() ,求证:
,求证:![]()

【答案】(1)①见解析;②△ABC面积的最大值是![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)①连接OB,OC,由圆的性质可得答案;
②先作AF⊥BC,垂足为点F,要使得面积最大,则当点A,O,D在同一直线上时取到
再根据三角形的面积公式即可得到答案;
(2)先设∠OED=∠ODE=α,∠COD=∠BOD=β,由锐角三角形性质得到
即![]() ,再结合题意及三角形内角和的性质得到
,再结合题意及三角形内角和的性质得到![]()
两式联立即可得到答案.
(1)①证明:连接OB,OC,
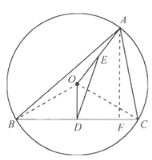
因为OB=OC,OD⊥BC,
所以∠BOD=![]() ∠BOC=
∠BOC=![]() ×2∠BAC=60°,
×2∠BAC=60°,
所以OD=![]() OB=
OB=![]() OA
OA
②作AF⊥BC,垂足为点F,
所以AF≤AD≤AO+OD=![]() ,等号当点A,O,D在同一直线上时取到
,等号当点A,O,D在同一直线上时取到
由①知,BC=2BD=![]() ,
,
所以△ABC的面积![]()
即△ABC面积的最大值是![]()
(2)设∠OED=∠ODE=α,∠COD=∠BOD=β,
因为△ABC是锐角三角形,
所以∠AOC+∠AOB+2∠BOD=360°,
即![]() (*)
(*)
又因为∠ABC<∠ACB,
所以∠EOD=∠AOC+∠DOC
![]()
因为∠OED+∠ODE+∠EOD=180°,
所以![]() (**)
(**)
由(*),(**),得![]() ,
,
即![]()


科目:初中数学 来源: 题型:
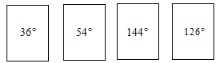
【题目】如图,有四张质地完全相同的卡片,正面分别写有四个角度,现将这四张卡片洗匀后,背面朝上.
(1)若从中任意抽取--张,求抽到锐角卡片的概宰;
(2)若从中任意抽取两张,求抽到的两张角度恰好互补的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b的图象经过点A(﹣2,6),且与x轴相交于点B,与正比例函数y=3x的图象相交于点C,点C的横坐标为1.
(1)求k、b的值;
(2)若点D在y轴负半轴上,且满足S△COD=![]() S△BOC,求点D的坐标.
S△BOC,求点D的坐标.
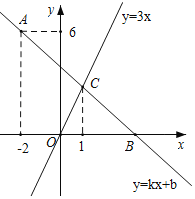
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,翻折∠C,使点C落在斜边AB上某一点D处,折痕为EF(点E,F分别在边AC,BC上),给出以下判断:①当CD⊥AB时,EF为△ABC的中位线;②当四边形CEDF为矩形时,AC=BC;③当点D为AB的中点时,△CEF与△ABC相似;④当△CEF与△ABC相似时,点D为AB的中点.其中正确的是_____(把所有正确的结论的序号都填在横线上).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+1交y轴于点A,交x轴正半轴于点B(4,0),与过A点的直线相交于另一点D(3,![]() ),过点D作DC⊥x轴,垂足为C.
),过点D作DC⊥x轴,垂足为C.
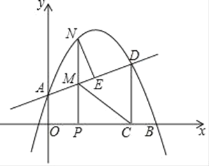
(1)求抛物线的表达式;
(2)点P在线段OC上(不与点O,C重合),过P作PN⊥x轴,交直线AD于M,交抛物线于点N,NE⊥AD于点E,求NE的最大值;
(3)若P是x轴正半轴上的一动点,设OP的长为t.是否存在t,使以点M,C,D,N为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.
(1)八(1)班抽中歌曲《我和我的祖国》的概率是__________;
(2)试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】九(1)班全体同学根据自己的爱好参加了六个兴趣小组(每个学生必须参加且只参加一个),为了了解学生参加兴趣小组的情况,班主任参加各个兴趣小组的人数进行了统计,绘制成了如图不完整的扇形统计图,已知参加“足球”小组的学生有7人,请解答下列问题:
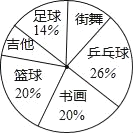
(1)九(1)班共有 名学生;
(2)若该班参加“吉他”小组与“街舞”小组的人数相同,请你计算,“吉他”小组对应扇形的圆心角的度数;
(3)若“足球”兴趣小组7个同学编号为1,2,3,4,5,6,7,把这些号码制成大小相同的号码球,放到A、B、C三个口袋中,A口袋中装有1,2,3三个号码球,B口袋中装4,5两个号码球,C口袋中装6,7两个号码球,从三个口袋中各随机取出1个球,请用列表法或树状图求取出的3个号码球都是奇数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市计划在十二年内通过公租房建设,解决低收入人群的住房问题.已知前7年,每年竣工投入使用的公租房面积y(单位:百万平方米)与时间x(第x年)的关系构成一次函数(1≤x≤7且x为整数),且第一和第三年竣工投入使用的公租房面积分别为![]() 和
和![]() 百万平方米;后5年每年竣工投入使用的公租房面积y(单位:百万平方米)与时间x(第x年)的关系是y=﹣
百万平方米;后5年每年竣工投入使用的公租房面积y(单位:百万平方米)与时间x(第x年)的关系是y=﹣![]() x+
x+![]() (7<x≤12且x为整数).
(7<x≤12且x为整数).
(1)已知第6年竣工投入使用的公租房面积可解决20万人的住房问题,如果人均住房面积,最后一年要比第6年提高20%,那么最后一年竣工投入使用的公租房面积可解决多少万人的住房问题?
(2)受物价上涨等因素的影响,已知这12年中,每年竣工投入使用的公租房的租金各不相同,且第一年,一年38元/m2,第二年,一年40元/m2,第三年,一年42元/m2,第四年,一年44元/m2……以此类推,分析说明每平方米的年租金和时间能否构成函数,如果能,直接写出函数解析式;
(3)在(2)的条件下,假设每年的公租房当年全部出租完,写出这12年中每年竣工投入使用的公租房的年租金W关于时间x的函数解析式,并求出W的最大值(单位:亿元).如果在W取得最大值的这一年,老张租用了58m2的房子,计算老张这一年应交付的租金.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某加工厂以每吨3000元的价格购进50吨原料进行加工.若进行粗加工,每吨加工费用为600元,需![]() 天,每吨售价4000元;若进行精加工,每吨加工费用为900元,需
天,每吨售价4000元;若进行精加工,每吨加工费用为900元,需![]() 天,每吨售价4500元.现将这50吨原料全部加工完.设其中粗加工x吨,获利y元.
天,每吨售价4500元.现将这50吨原料全部加工完.设其中粗加工x吨,获利y元.
(1)请完成表格并求出y与x的函数关系式(不要求写自变量的范围);
表一
粗加工数量/吨 | 3 | 7 | x |
精加工数量/吨 | 47 |
|
|
表二
粗加工数量/吨 | 3 | 7 | x |
粗加工获利/元 |
| 2800 |
|
精加工获利/元 |
| 25800 |
|
(2)如果必须在20天内完成,如何安排生产才能获得最大利润,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com