
【题目】九(1)班全体同学根据自己的爱好参加了六个兴趣小组(每个学生必须参加且只参加一个),为了了解学生参加兴趣小组的情况,班主任参加各个兴趣小组的人数进行了统计,绘制成了如图不完整的扇形统计图,已知参加“足球”小组的学生有7人,请解答下列问题:
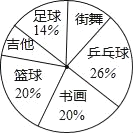
(1)九(1)班共有 名学生;
(2)若该班参加“吉他”小组与“街舞”小组的人数相同,请你计算,“吉他”小组对应扇形的圆心角的度数;
(3)若“足球”兴趣小组7个同学编号为1,2,3,4,5,6,7,把这些号码制成大小相同的号码球,放到A、B、C三个口袋中,A口袋中装有1,2,3三个号码球,B口袋中装4,5两个号码球,C口袋中装6,7两个号码球,从三个口袋中各随机取出1个球,请用列表法或树状图求取出的3个号码球都是奇数的概率.
【答案】(1)50;(2)36°;(3)见解析,![]()
【解析】
(1)首先设共有x人,然后由题意可得14%x=7,继而求得答案;
(2)首先设参加“吉他”小组与“街舞”小组的人所占百分比为a,可得2a+14%+20%+20%+26%=1,继而求得答案;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与取出的3个号码球都是奇数的情况,再利用概率公式即可求得答案.
解:(1)设共有x人,
14%x=7,
解得:x=50;
故答案为:50;
(2)设参加“吉他”小组与“街舞”小组的人所占百分比为a,
则2a+14%+20%+20%+26%=1,
∴a=10%,
故“吉他”小组对应扇形的圆心θ=10%×360°=36°
(3)树状图:如图所示
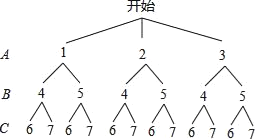
∵由树状图可以看出,所有可能出现的结果共有12种,这些结果出现的可能性相等.其中3个号码都是奇数的结果有:1 5 7 和3 5 7两种.
∴P(3个奇数)=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】今年4月22日是第50个世界地球日,某校在八年级5个班中,每班各选拔10名学生参加“环保知识竞赛”并评出了一、二、三等奖各若干名,学校将获奖情况绘成如图所示的不完整的条形统计图和扇形统计图,请你根据图中信息解答下列问题:
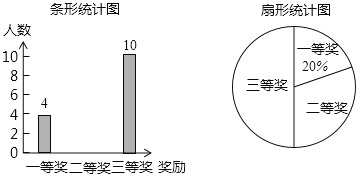
(1)求本次竞赛获奖的总人数,并补全条形统计图;
(2)求扇形统计图中“二等奖”所对应扇形的圆心角度数;
(3)已知甲、乙、丙、丁4位同学获得一等奖,学校将采取随机抽签的方式在4人中选派2人参加上级团委组织的“爱护环境、保护地球”知识竞赛,请求出抽到的2人恰好是甲和乙的概率(用画树状图或列表等方法求解).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,∠B=90°,
中,∠B=90°,![]() ,点D,E分别是边BC,AC的中点,连接
,点D,E分别是边BC,AC的中点,连接![]() 将
将![]() 绕点C按顺时针方向旋转,记旋转角为
绕点C按顺时针方向旋转,记旋转角为![]() .
.
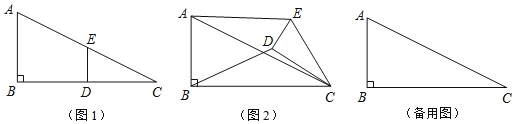
![]() 问题发现:
问题发现:
![]() 当
当![]() 时,
时,![]() _____;
_____;![]() 当
当![]() 时,
时,![]() _____.
_____.
![]() 拓展探究:
拓展探究:
试判断:当![]() 时,
时,![]() 的大小有无变化?请仅就图2的情况给出证明.
的大小有无变化?请仅就图2的情况给出证明.
![]() 问题解决:
问题解决:
当![]() 旋转至A、D、E三点共线时,直接写出线段BD的长.
旋转至A、D、E三点共线时,直接写出线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知锐角![]() 内接于⊙O,
内接于⊙O, ![]() 于点D,连结AO.
于点D,连结AO.
⑴若![]() .
.
①求证:![]() ;
;
②当![]() 时,求
时,求![]() 面积的最大值;
面积的最大值;
⑵点E在线段OA上,![]() ,连接DE,设
,连接DE,设![]() ,
,![]() (m、n是正数),若
(m、n是正数),若![]() ,求证:
,求证:![]()

查看答案和解析>>
科目:初中数学 来源: 题型:
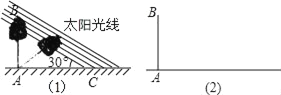
【题目】某数学兴趣小组,利用树影测量树高,如图(1),已测出树AB的影长AC为12米,并测出此时太阳光线与地面成30°夹角.
(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变.求树的最大影长.(用图(2)解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在一次射击比赛中各射靶5次,两人成绩的条形统计图如图所示,则下列说法正确的是( )
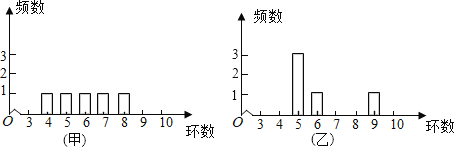
A.甲的成绩的平均数小于乙的成绩的平均数
B.甲的成绩的中位数等于乙的成绩的中位数
C.甲的成绩的极差小于乙的成绩的极差
D.甲的成绩的方差小于乙的成绩的方差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=﹣x2+2tx+2.
(1)求抛物线的对称轴(用含t的代数式表示);
(2)将点A(﹣1,3)向右平移5个单位长度,得到点B.
①若抛物线经过点B求t的值;
②若抛物线与线段AB恰有一个交点,结合函数图象直接写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在Rt△ABC中,∠BAC=90°,CD为∠ACB的平分线,将∠ACB沿CD所在的直线对折,使点B落在点B′处,连结AB',BB',延长CD交BB'于点E,设∠ABC=2α(0°<α<45°).

(1)如图1,若AB=AC,求证:CD=2BE;
(2)如图2,若AB≠AC,试求CD与BE的数量关系(用含α的式子表示);
(3)如图3,将(2)中的线段BC绕点C逆时针旋转角(α+45°),得到线段FC,连结EF交BC于点O,设△COE的面积为S1,△COF的面积为S2,求![]() (用含α的式子表示).
(用含α的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com