
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
九(1)班数学兴趣小组经 过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
| 时间x(天) | 1≤x<50 | 50≤x≤90 |
| 售价(元/件) | x+40 | 90 |
| 每天销量(件) | 200﹣2x |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?
查看答案和解析>>
科目:初中数学 来源: 题型:
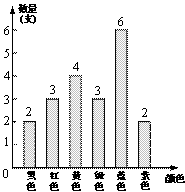
有一盒水彩笔除了颜色外无其他差别,其中各种颜色的数量统计如图所示.小腾在无法看到盒中水彩笔颜色的情形下随意抽出一支.小腾抽到蓝色水彩笔的概率为
A.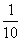 B.
B.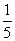
 C.
C.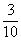 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知二次函数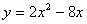 .
.
(1) 用配方法将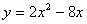 化成
化成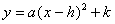 的形式;
的形式;
(2) 求出该二次函数的图象与x轴的交点A,B的坐标(A在B的左侧);
(3) 将该二次函数的图象沿x轴向左平移2个单位,再沿y轴向上平移3个单位,请直接写出得到的新图象的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
在平面直角坐标系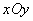 中,⊙C的半径为r,点P是与圆心C不重合的点,给出如下定义:若点
中,⊙C的半径为r,点P是与圆心C不重合的点,给出如下定义:若点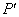 为射线CP上一点,满足
为射线CP上一点,满足
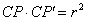 ,则称点
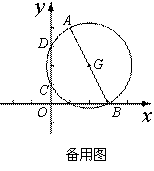
,则称点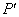 为点P关于⊙C的反演点.右图为点P及其关于⊙C的反演点
为点P关于⊙C的反演点.右图为点P及其关于⊙C的反演点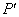 的示意图.
的示意图.
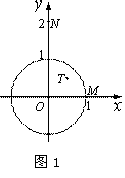
(1) 如图1,当⊙O的半径为1时,分别求出点M(1,0),N(0,2),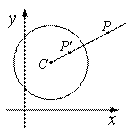
T(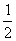 ,
,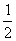 )关于⊙O的反演点
)关于⊙O的反演点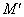 ,
,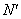 ,
,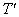 的坐标;
的坐标;
(2) 如图2,已知点A(1,4),B(3,0),以AB为直径的⊙G与y轴交于点C,D(点C位于点D下方),E为CD的中点.
① 若点O,E关于⊙G的反演点分别为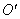 ,
,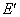 ,求∠
,求∠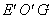 的大小;
的大小;
 ② 若点P在⊙G上,且∠BAP=∠OBC,设直线AP与x轴的交点为Q,点Q关于⊙G的反演点为
② 若点P在⊙G上,且∠BAP=∠OBC,设直线AP与x轴的交点为Q,点Q关于⊙G的反演点为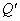 ,请直接写出线段
,请直接写出线段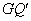 的长度.
的长度.
 | |||
 | |||
查看答案和解析>>
科目:初中数学 来源: 题型:
学习直线、射线、线段和线段中点等内容之后,王老师请同学们交流这样一个问题:“射线OA上有B,C两点,若OB=8,BC=2,点D是线段OB的中点,请你求出线段DC的长.”张华同学通过计算得到DC的长是6,你认为张华的答案是否正确 ,你的理由是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
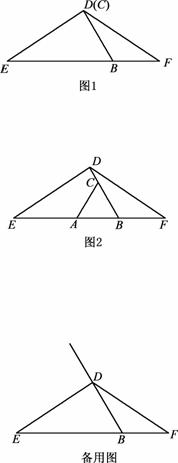
在△DEF中,DE=DF,点B在EF边上,且∠EBD=60°,C是射线BD上的一个动点(不与点B重合,且BC≠BE),在射线BE上截取BA=BC,连接AC.
(1)当点C在线段BD上时,
①若点C与点D重合,请根据题意补全图1,并直接写出线段AE与BF的数量关系为 ;
②如图2,若点C不与点D重合,请证明AE=BF+CD;
(2)当点C在线段BD的延长线上时,用等式表示线段AE ,BF ,CD之间的数量关系(直接写出结果,不需要证明).
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com