
【题目】正方形OABC的边长为4,对角线相交于点P,抛物线L经过O,P,A三点,点E是正方形内的抛物线上的动点.
(1)建立适当的平面直角坐标系.
①直接写出O,P,A三点坐标;
②求抛物线L的表达式;
(2)求△OAE与△OCE面积之和的最大值.
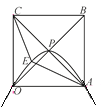
【答案】(1)建立平面直角坐标系见解析,①点O的坐标为(0,0),点A的坐标为(4,0),点P的坐标为(2,2);②抛物线L的表达式为y=-![]() x2+2x;(2)△OAE与△OCE面积之和最大值为9.
x2+2x;(2)△OAE与△OCE面积之和最大值为9.
【解析】试题分析:(1)以O点为原点,线段OA所在的直线为x轴,线段OC所在的直线为y轴建立直角坐标系.①根据正方形的边长结合正方形的性质即可得出点O、P、A三点的坐标;②设抛物线L的解析式为y=ax2+bx+c,结合点O、P、A的坐标利用待定系数法即可求出抛物线的解析式;(2)由点E为正方形内的抛物线上的动点,设出点E的坐标,结合三角形的面积公式找出S△OAE+SOCE关于m的函数解析式,根据二次函数的性质即可得出结论.
试题解析:(1)以O点为原点,线段OA所在的直线为x轴,线段OC所在的直线为y轴建立直角坐标系,如图所示.
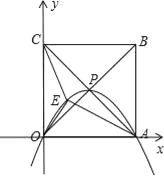
①∵正方形OABC的边长为4,对角线相交于点P,
∴点O的坐标为(0,0),点A的坐标为(4,0),点P的坐标为(2,2).
②设抛物线L的解析式为y=ax2+bx+c, ∵抛物线L经过O、P、A三点,
∴有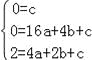 , 解得:
, 解得: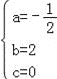 , ∴抛物线L的解析式为y=﹣
, ∴抛物线L的解析式为y=﹣![]() +2x.
+2x.
(2)∵点E是正方形内的抛物线上的动点, ∴设点E的坐标为(m,﹣![]() +2m)(0<m<4),
+2m)(0<m<4),
∴S△OAE+SOCE=![]() OAyE+
OAyE+![]() OCxE=﹣m2+4m+2m=﹣(m﹣3)2+9,
OCxE=﹣m2+4m+2m=﹣(m﹣3)2+9,
∴当m=3时,△OAE与△OCE面积之和最大,最大值为9.


 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,点E在⊙O上,C为![]() 的中点,过点C作直线CD⊥AE于D,连接AC,BC.
的中点,过点C作直线CD⊥AE于D,连接AC,BC.
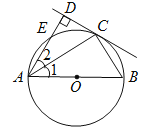
(1)试判断直线CD与⊙O的位置关系,并说明理由;
(2)若AD=2,AC=![]() ,求AB的长.
,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,已知菱形ABCD的面积为15,顶点A在双曲线![]() 上,CD与y轴重合,且AB⊥x轴于B,AB=5.
上,CD与y轴重合,且AB⊥x轴于B,AB=5.
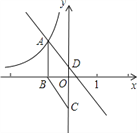
(1)求顶点A的坐标和k的值;
(2)求直线AD的解析式y1;
(3)在第二象限内,比较y与y1 的大小。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平行四边形ABCD中,CE平分∠BCD且交AD于点E,A F∥CE,且交BC于点F.
(1)求证:△ABF≌△CDE;
(2)如图,若∠1=65°,求∠B的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红把班级勤工助学挣得的班费500元按一年期存入银行,已知年利率为x,一年到期后银行将本金和利息自动按一年定期转存,设两年到期后,本、利和为y元,则y与x之间的函数关系式为( )
A. y=500(x+1)2 B. y=x2+500 C. y=x2+500x D. y=x2+5x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com