
【题目】含45°角的直角三角板如图放置在平面直角坐标系中,其中A(﹣2,0),B(0,1),则直线BC的解析式为 . 
【答案】y=﹣ ![]() x+1
x+1
【解析】解: 如图,过C作CD⊥x轴于点D,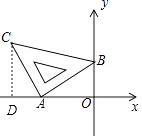
∵∠CAB=90°,
∴∠DAC+∠BAO=∠BAO+∠ABO=90°,
∴∠DAC=∠ABO,
在△AOB和△CDA中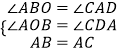
∴△AOB≌△CDA(AAS),
∵A(﹣2,0),B(0,1),
∴AD=BO=1,CD=AO=2,
∴C(﹣3,2),
设直线BC解析式为y=kx+b,
∴ ![]() ,解得
,解得 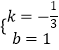 ,
,
∴直线BC解析式为y=﹣ ![]() x+1,
x+1,
所以答案是:y=﹣ ![]() x+1.
x+1.
【考点精析】掌握确定一次函数的表达式是解答本题的根本,需要知道确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
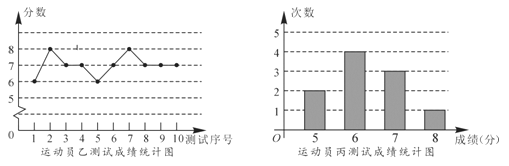
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
运动员甲测试成绩表

(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么? (参考数据:三人成绩的方差分别为![]() 、
、![]() 、
、![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图AB∥CD.∠1=∠2,∠3=∠4,试说明AD∥BE.

解:∵AB∥CD(已知)
∴∠4=∠ ( )
∵∠3=∠4(已知)
∴∠3=∠ ( )
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF(
即∠ =∠ ( )
∴∠3=∠
∴AD∥BE( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为丰富学生的校园生活,准备从某体育用品商店一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买3个足球和2个篮球共需310元,购买2个足球和5个篮球共需500元.
(1)购买一个足球,一个篮球各需多少元?
(2)根据学校的实际情况,需从该体育用品商店一次性购买足球和篮球共96个,要求购买足球和篮球的总费用不超过5720元,这所中学最多可以购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的统计图表示某体校射击队甲、乙两名队员射击比赛的成绩.根据统计图中的信息可得,下列结论正确的是( )

A. 甲队员成绩的平均数比乙队员的大
B. 甲队员成绩的方差比乙队员的大
C. 甲队员成绩的中位数比乙队员的大
D. 乙队员成绩的方差比甲队员的大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经营A种品牌的玩具,购进时间的单价是30元,但据市场调查,在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请用含x的代数式表示该玩具的销售量;
(2)若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于450件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
(3)该商场计划将(2)中所得的利润的一部分资金采购一批B种玩具并转手出售,根据市场调查并准备两种方案,方案①:如果月初出售,可获利15%,并可用本和利再投资C种玩具,到月末又可获利10%;方案②:如果只到月末出售可直接获利30%,但要另支付他库保管费350元,请问商场如何使用这笔资金,采用哪种方案获利较多?
查看答案和解析>>
科目:初中数学 来源: 题型:
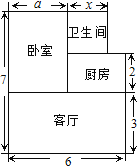
【题目】张先生准备在沙坪坝购买一套小户型商品房,他去某楼盘了解情况得知,该户型商品房的单价是12000元/m2,面积如图所示(单位:米,卧室的宽为a米,卫生间的宽为x米),
(1) 用含a和x的式子表示该户型的面积
(2) 售房部为张先生提供了以下两种优惠方案:
方案一:整套房的单价是12 000元/m2,其中厨房只算![]() 的面积;
的面积;
方案二:整套房按原销售总金额的9折出售,
若张先生购买的户型a=3,且分别用两种方案购房金额相等,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,∠C=70°,△AB′C′与△ABC 关于直线 EF对称,∠CAF=10°,连接 BB′,则∠ABB′的度数是( )

A. 30° B. 35° C. 40° D. 45°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com