
【题目】某公司销售一种服装,进价120元/件,售价200元/件,公司对大量购买有优惠政策,凡是一次性购买20件以上的,每多买一件,售价就降低1元.设顾客购买![]() (件)时公司的利润为
(件)时公司的利润为![]() (元).
(元).
(1)当一次性购买![]() 件
件![]() 时,
时,
①售价为 元/件;
②求![]() (元)与
(元)与![]() (件)之间的函数表达式
(件)之间的函数表达式
在此优惠政策下,顾客购买多少件时公司能够获得最大利润?
(2) 设售价为![]() 元/件,求
元/件,求![]() 在什么范围内才能保证公司每次卖的越多,利润也越多.
在什么范围内才能保证公司每次卖的越多,利润也越多.
【答案】(1)①220﹣x;②y=﹣x2+100x,③当顾客购买50件时,获得最大利润2500元;(2)170≤a≤200
【解析】试题分析:(1)①根据题意列出代数式即可;②根据题意即可的结论;(2)根据y=-x2+100x=-(x-50)2+2500,于是得到抛物线的开口向下,x=50时,y有最大值,在对称轴x=50的左侧,y随x的增大而增大,可得到结论;
试题解析:
(1)①220﹣x;
②y=(220﹣x﹣120)x=﹣x2+100x,
③y=﹣x2+100x=﹣(x﹣50)2+2500
∴当顾客购买50件时,获得最大利润2500元
(2)①当0<x≤20时,y= (200-120) x=80x,y随x的增大而增大,此时a=200元/件 ②当x>20时,由(1)得y=-x2+100x=-(x-50)2+2500
当20<x≤50时,y随x的增大而增大
∴只有20<x≤50时,才每次卖的越多,利润也越多
由题意a=220-x,a随x的增大而减小
当x=50时,a=170,所以当每次卖的越多,利润也越多时,a≥170
又∵a<200,所 以170≤a<200
综上170≤a≤200


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE且交AG于点F. 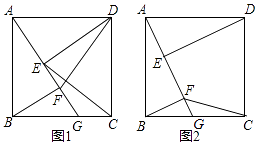
(1)求证:AE=BF;
(2)如图1,连接DF、CE,探究线段DF与CE的关系并证明;
(3)如图2,若AB= ![]() ,G为CB中点,连接CF,直接写出四边形CDEF的面积为 .
,G为CB中点,连接CF,直接写出四边形CDEF的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用电脑,在同一页面对某图形进行复制,得到一组图案,这一组图案可以看作一个基本图形通过( )得到的
A. 旋转 B. 平移和旋转
C. 平移 D. 拉伸
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算正确的是( )
A.﹣2(x+3y)=﹣2x+3y
B.﹣2(x+3y)=﹣2x﹣3y
C.﹣2(x+3y)=﹣2x+6y
D.﹣2(x+3y)=﹣2x﹣6y
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是正方形ABCD内的一点,连接CP,将线段CP绕点C顺时针旋转90°,得到线段CQ,连接BP,DQ.
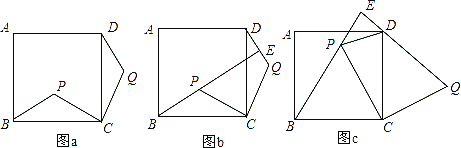
(1)、如图a,求证:△BCP≌△DCQ;
(2)、如图,延长BP交直线DQ于点E.
①如图b,求证:BE⊥DQ;
②如图c,若△BCP为等边三角形,判断△DEP的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com