
【题目】如图,四边形ABCD是正方形,点G是BC边上任意一点,DE⊥AG于点E,BF∥DE且交AG于点F. 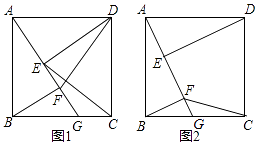
(1)求证:AE=BF;
(2)如图1,连接DF、CE,探究线段DF与CE的关系并证明;
(3)如图2,若AB= ![]() ,G为CB中点,连接CF,直接写出四边形CDEF的面积为 .
,G为CB中点,连接CF,直接写出四边形CDEF的面积为 .
【答案】
(1)证明:∵DE⊥AG于点E,BF∥DE且交AG于点F,
∴BF⊥AG于点F,
∴∠AED=∠BFA=90°,
∵四边形ABCD是正方形,
∴AB=AD且∠BAD=∠ADC=90°,
∴∠BAF+∠EAD=90°,
∵∠EAD+∠ADE=90°,
∴∠BAF=∠ADE,
在△AFB和△DEA中,
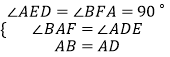 ,
,
∴△AFB≌△DEA(AAS),
∴BF=AE
(2)证明:DF=CE且DF⊥CE.
理由如下:∵∠FAD+∠ADE=90°,∠EDC+∠ADE=∠ADC=90°,
∴∠FAD=∠EDC,
∵△AFB≌△DEA,
∴AF=DE,
又∵四边形ABCD是正方形,
∴AD=CD,
在△FAD和△EDC中,
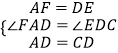 ,
,
∴△FAD≌△EDC(SAS),
∴DF=CE且∠ADF=∠DCE,
∵∠ADF+∠CDF=∠ADC=90°,
∴∠DCE+∠CDF=90°,
∴DF⊥CE
(3)3
【解析】(3)∵AB= ![]() ,G为CB中点, ∴BG=
,G为CB中点, ∴BG= ![]() BC=
BC= ![]() ,
,
由勾股定理得,AG= ![]() =
= ![]() =
= ![]() ,
,
∵S△ABG= ![]() AGBF=
AGBF= ![]() ABBG,
ABBG,
∴ ![]() ×
× ![]() BF=
BF= ![]() ×
× ![]() ×
× ![]() ,
,
解得BF= ![]() ,
,
由勾股定理得,AF= ![]() =
= ![]() =
= ![]() ,
,
∵△AFB≌△DEA,
∴AE=BF= ![]() ,
,
∴AE=EF= ![]() ,
,
∴DE垂直平分AF,
∴DF=AD= ![]() ,
,
由(2)知,DF=CE且DF⊥CE,
∴四边形CDEF的面积= ![]() DFCE=
DFCE= ![]() ×
× ![]() ×
× ![]() =3.
=3.
所以答案是:3.
【考点精析】本题主要考查了正方形的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
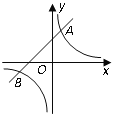
【题目】如图,反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于
的图象交于![]() ,
,![]() 两点.
两点.
(1)求反比例函数与一次函数的解析式;
(2)根据图象回答:当![]() 取何值时,反比例函数的值大于一次函数的值.
取何值时,反比例函数的值大于一次函数的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司销售一种服装,进价120元/件,售价200元/件,公司对大量购买有优惠政策,凡是一次性购买20件以上的,每多买一件,售价就降低1元.设顾客购买![]() (件)时公司的利润为
(件)时公司的利润为![]() (元).
(元).
(1)当一次性购买![]() 件
件![]() 时,
时,
①售价为 元/件;
②求![]() (元)与
(元)与![]() (件)之间的函数表达式
(件)之间的函数表达式
在此优惠政策下,顾客购买多少件时公司能够获得最大利润?
(2) 设售价为![]() 元/件,求
元/件,求![]() 在什么范围内才能保证公司每次卖的越多,利润也越多.
在什么范围内才能保证公司每次卖的越多,利润也越多.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中选两个作为补充条件,使ABCD为正方形(如图),现有下列四种选法,你认为其中错误的是( ) 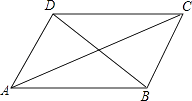
A.①②
B.②③
C.①③
D.②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() .
.
(1)若该反比例函数的图象与直线![]() (
(![]() ≠0)只有一个公共点,求
≠0)只有一个公共点,求![]() 的值;
的值;
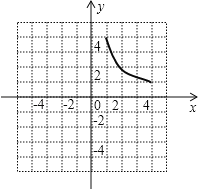
(2)如图,反比例函数![]() 的图象记为曲线
的图象记为曲线![]() ,将
,将![]() 向左平移2个单位长度,得曲线
向左平移2个单位长度,得曲线![]() ,请在图中画出
,请在图中画出![]() ,并直接写出
,并直接写出![]() 平移至
平移至![]() 处 所扫过的面积.
处 所扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一张复印出来的纸上,一个三角形的一条边由原图中的2cm变成了6cm,则复印出的三角形的面积是原图中三角形面积的( )
A. 3倍B. 6倍C. 9倍D. 12倍
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com