
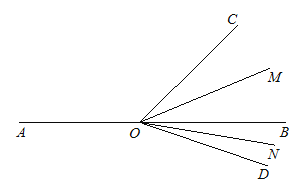
【题目】如图,已知点O为直线AB上一点,射线OC和OD在直线AB的两侧,∠BOC=40°,∠BOD=20°,OM、ON分别平分∠BOC、∠BOD,射线OC以4°/秒的速度绕点O顺时针匀速旋转,射线OD以2°/秒的速度绕点O逆时针匀速旋转.设运动时间为t秒(0<t<100).
(1)运动开始前,∠MON的度数是多少?请写出计算过程.
(2)当t为多少时,∠BOM=8°?请写出计算过程.
(3)当t为多少时,射线OM和射线ON在同一条直线上?请写出计算过程.
【答案】(1)∠MON=30°;(2)t的值为6或14时,∠BOM=8°;(3)t的值为10或70.
【解析】试题分析:(1)由角平分线定义可得:∠MON=![]() ∠COD,由此即可得到结论;
∠COD,由此即可得到结论;
(2)由∠BOM的度数得到∠BOC的度数,解方程40-4t=16或4t-40=16即可得到结论;
(3)分两种情况讨论:①当OM与ON重合时,即OC与OD重合在一起;②当OM与ON互为反向延长线上时.
试题解析:解:(1)∵OM平分∠BOC,∴∠BOM=![]() ∠BOC.
∠BOC.
同理∠BON=![]() ∠BOD,∴∠MON=∠BOM+∠BON=
∠BOD,∴∠MON=∠BOM+∠BON=![]() ∠BOC+
∠BOC+![]() ∠BOD=
∠BOD=![]() ∠COD.
∠COD.
∵∠COD=∠BOC+∠BOD=60°,∴∠MON=30°.
(2)∵∠BOM=![]() ∠BOC=8°,∴∠BOC=16°,∴40-4t=16或4t-40=16,解得t=6或t=14.
∠BOC=8°,∴∠BOC=16°,∴40-4t=16或4t-40=16,解得t=6或t=14.
答:t的值为6或14时,∠BOM=8°.
(3)①当OM与ON重合时,即OC与OD重合在一起,有4t+2t=60, 解得t=10.
②当OM与ON互为反向延长线上时, 有 2t+t=180+30,解得:t=70.
答:t的值为10或70.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
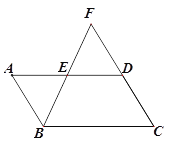
【题目】如图,□ABCD中,E为AD的中点,BE、CD相交于点F.
(1)求证:AB=DF
(2)若△DEF的面积为S1,△BCF的面积为S2,且S12-S2+4=0,求□ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
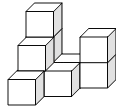
【题目】如图,在平整地面上,若干个完全相同的棱长为10cm的小正方体堆成一个几何体.
(1)这个几何体由______个小正方体组成.
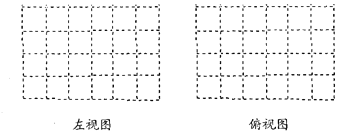
(2)在下面网格中画出左视图和俯视图.
(3)如果在这个几何体的表面(不含底面)喷上黄色的漆,则这个几何体喷漆的面积是多少cm2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】笔尖在纸上快速滑动写出了一个又一个字,这说明了;车轮旋转时,看起来像一个整体的圆面,这说明了;直角三角形绕它的直角边旋转一周形成了一圆锥体,这说明了.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列算式:21=2,22=4,23=8,24=16,25=32,26=64,27=128,通过观察,用你所发现的规律确定22011的个位数字是( )
A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动.在一个不透明的箱子里放有4个完全相同的小球,球上分别标有“0元”、“10元”、“30元”和“50元”的字样.规定:顾客在本商场同一日内,消费每满300元,就可以从箱子里先后摸出两个球(每次只摸出一个球,第一次摸出后不放回).商场根据两个小球所标金额之和返还相应价格的购物券,可以重新在本商场消费.某顾客消费刚好满300元,则在本次消费中:
(1)该顾客至少可得___元购物券,至多可得___元购物券;
(2)请用画树状图或列表法,求出该顾客所获购物券的金额不低于50元的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com