
【题目】某商场为了吸引顾客,设计了一种促销活动.在一个不透明的箱子里放有4个完全相同的小球,球上分别标有“0元”、“10元”、“30元”和“50元”的字样.规定:顾客在本商场同一日内,消费每满300元,就可以从箱子里先后摸出两个球(每次只摸出一个球,第一次摸出后不放回).商场根据两个小球所标金额之和返还相应价格的购物券,可以重新在本商场消费.某顾客消费刚好满300元,则在本次消费中:
(1)该顾客至少可得___元购物券,至多可得___元购物券;
(2)请用画树状图或列表法,求出该顾客所获购物券的金额不低于50元的概率.
【答案】(1)10,80
【解析】分析:(1)根据题意即可求得该顾客至少可得的购物券,至多可得的购物券的金额;(2)首先根据题意列出表格,然后由表格求得所有等可能的结果与该顾客所获购物券的金额不低于50元的情况,再利用概率公式求解即可求得答案.
本题解析:.(1)10,80;(2)![]()
(2)方法一:树状图法:
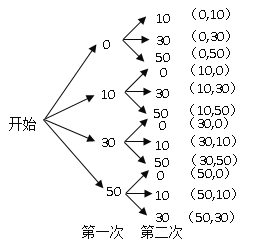
方法二:列表法:
0 | 10 | 30 | 50 | |
0 | (0,10) | (0,30) | (0,50) | |
10 | (10,0) | (10,30) | (10,50) | |
30 | (30,0) | (30,10) | (30,50) | |
50 | (50,0) | (50,10) | (50,30) |
从上面的树状图或表格可以看出,两次摸球可能出现的结果共有12种,
每种结果出现的可能性相同,而所获购物券的金额不低于50元的结果
共有6种.
所以该顾客所获购物券的金额不低于50元的概率是![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
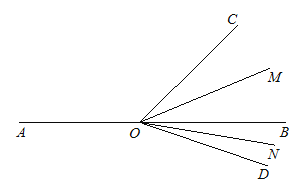
【题目】如图,已知点O为直线AB上一点,射线OC和OD在直线AB的两侧,∠BOC=40°,∠BOD=20°,OM、ON分别平分∠BOC、∠BOD,射线OC以4°/秒的速度绕点O顺时针匀速旋转,射线OD以2°/秒的速度绕点O逆时针匀速旋转.设运动时间为t秒(0<t<100).
(1)运动开始前,∠MON的度数是多少?请写出计算过程.
(2)当t为多少时,∠BOM=8°?请写出计算过程.
(3)当t为多少时,射线OM和射线ON在同一条直线上?请写出计算过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国2016年第一季度GDP总值经初步核算大约为159000亿元,数据159000用科学记数法表示为( )
A.1.59×104
B.1.59×105
C.1.59×104
D.15.9×104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在不透明的布袋中,装有大小、形状完全相同的3个黑球、2个红球,从中摸一个球,摸出的是个黑球,这一事件是( )
A.必然事件B.随机事件C.确定事件D.不可能事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,有A(2,﹣1),B(0,2),C(2,0),D(﹣2,1)四点,其中关于原点对称的两点为( )
A.点A和点BB.点B和点CC.点C和点DD.点D和点A
查看答案和解析>>
科目:初中数学 来源: 题型:
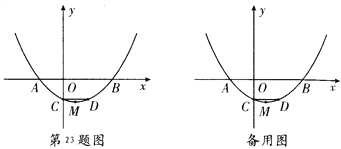
【题目】如图,已知抛物线y=![]() (x+2)(x-4)与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C.CD∥x轴,交抛物线于点D,M为抛物线的顶点.
(x+2)(x-4)与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C.CD∥x轴,交抛物线于点D,M为抛物线的顶点.
(l)求点A、B、C的坐标;
(2)设动点N( -2,n),求使MN+BN的值最小时n的值:
(3)P是抛物线上一点,请你探究:是否存在点P,使以P、A、B为顶点的三角形与△ABD相似(△PAB与△ABD不重合)? 若存在,写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com