
【题目】如图,矩形ABCD的对角线AC、BD相交于点O,∠AOB=120°,CE∥BD,DE∥AC,若AD=4,则四边形CODE的周长 . 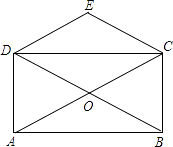
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动.在一个不透明的箱子里放有4个完全相同的小球,球上分别标有“0元”、“10元”、“30元”和“50元”的字样.规定:顾客在本商场同一日内,消费每满300元,就可以从箱子里先后摸出两个球(每次只摸出一个球,第一次摸出后不放回).商场根据两个小球所标金额之和返还相应价格的购物券,可以重新在本商场消费.某顾客消费刚好满300元,则在本次消费中:
(1)该顾客至少可得___元购物券,至多可得___元购物券;
(2)请用画树状图或列表法,求出该顾客所获购物券的金额不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
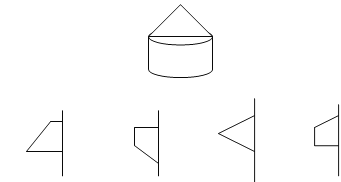
【题目】如图是一个粮仓,已知粮仓底面直径为8m,粮仓顶部顶点到地面的垂直距离为9m,粮仓下半部分高为6m,观察并回答下列问题:
(1)粮仓是由两个几何体组成的,他们分别是________;
(2)用一个平面去截粮仓,截面可能是____________(写出一个即可);
(3)如图,将下面的图形分别绕虚线旋转一周,哪一个能形成粮仓?用线连一连;
(4)求出该粮仓的容积(结果精确到0.1, ![]() 取3.14).
取3.14).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=80°,∠B=40°,D,E分别是AB,AC上的点,且DE∥BC,则∠AED的度数为( )

A. 40° B. 60° C. 80° D. 120°
查看答案和解析>>
科目:初中数学 来源: 题型:
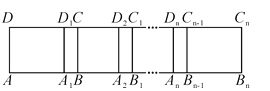
【题目】如图,长方形ABCD中,AB=6,第一次平移长方形ABCD沿AB的方向向右平移5个单位长度,得到长方形A1B1C1D1,第2次平移长方形A1B1C1D1沿A1B1的方向向右平移5个单位长度,得到长方形A2B2C2D2,…,第n次平移长方形An-1Bn-1Cn-1Dn-1沿An-1Bn-1的方向向右平移5个单位长度,得到长方形AnBnCnDn(n>2),若ABn的长度为2 016,则n的值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,且AB =6,C是⊙O上一点,D是![]() 的中点,过点D作⊙O的切线,与AB、AC的延长线分别交于点E、F,连接AD.
的中点,过点D作⊙O的切线,与AB、AC的延长线分别交于点E、F,连接AD.
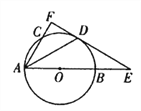
(l)求证:AF⊥EF;
(2)填空:
①当BE= 时,点C是AF的中点;
②当BE= 时,四边形OBDC是菱形,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=-x-1与反比例函数y=kx-1的图象都过点A(m,1).
(1)求m的值,并求反比例函数的解析式;
(2)求正比例函数与反比例函数的另一个交点B的坐标;
(3)求△AOB的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com