
【题目】已知一次函数y=-x-1与反比例函数y=kx-1的图象都过点A(m,1).
(1)求m的值,并求反比例函数的解析式;
(2)求正比例函数与反比例函数的另一个交点B的坐标;
(3)求△AOB的面积。
【答案】(1)m=-2, ![]() ;(2)B(1,-2);(3)1.5.
;(2)B(1,-2);(3)1.5.
【解析】试题分析:(1)将A(m,1)代入y=-x-1即可求出m的值,把所得A点坐标代入反比例函数解析式即可求出k的值,从而得到反比例函数解析式;(2)将正比例函数和反比例函数的解析式组成方程组,其解即为函数图象的交点坐标;(3)画出函数图象,根据A、B的坐标及直线AB和x轴的交点坐标利用三角形的面积公式求解.
试题解析:
(1)将A(m,1)代入y=-x-1得,-m-1=1,解得m=-2.
∴A点坐标为(-2,1).
将(-2,1)代入y=![]() 得,k=(-2)×1=-2.
得,k=(-2)×1=-2.
∴反比例函数解析式为y=![]()
(2)将正比例函数y=-x-1和反比例函数解析式y=![]() 组成方程组得,
组成方程组得,
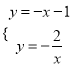
解得![]() ,
, ![]() ,
,
∴B点坐标为(1,-2);
(3)直线AB解析式为y=-x-1,与y轴交点坐标C(-1,0)
∴S△AOB=S△AOC+S△BOC=1.5.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:初中数学 来源: 题型:
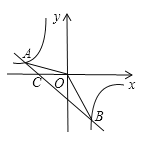
【题目】如图,已知抛物线y=![]() (x+2)(x-4)与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C.CD∥x轴,交抛物线于点D,M为抛物线的顶点.
(x+2)(x-4)与x轴交于点A、B(点A位于点B的左侧),与y轴交于点C.CD∥x轴,交抛物线于点D,M为抛物线的顶点.
(l)求点A、B、C的坐标;
(2)设动点N( -2,n),求使MN+BN的值最小时n的值:
(3)P是抛物线上一点,请你探究:是否存在点P,使以P、A、B为顶点的三角形与△ABD相似(△PAB与△ABD不重合)? 若存在,写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先化简,再求值:
(1)(x+y)(x-y)-x(x+y)+2xy,其中x=1,y=2.
(2)[(2x-y )2+(2x+y)(2x-y)-4xy]÷8x,其中x,y满足|x-3|+(y+2 )2=0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com