练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知一元二次方程x2+mx+m﹣1=0有两个相等的实数根，则m= ．

    【答案】2
    【解析】解：∵关于x的一元二次方程x2﹣mx+m﹣1=0有两个相等的实数根，
    ∴△=b2﹣4ac=m2﹣4×1×（m﹣1）=m2﹣4m+4=（m﹣2）2=0，
    ∴m=2，
    故答案为：2．
    首先根据原方程根的情况，利用根的判别式求出m的值即可．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图,△ABC是边长为a的等边三角形,P是△ABC内的任意一点,过点P作EF∥AB分别交AC,BC于点E,F,过点P作GH∥BC分别交AB,AC于点G,H,过点P作MN∥AC分别交AB,BC于点M,N,猜想EF+GH+MN的值是多少.其值是否随点P位置的改变而改变?并说明理由.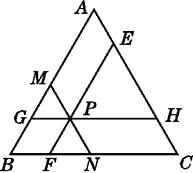

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了迎接杭州G20峰会,某校开展了设计“YJG20”图标的活动,下列图形中既是轴对称图形又是中心对称图形的是( )
    A.
    B.
    C.
    D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

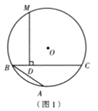
    【题目】阿基米德折弦定理：如图1，AB和BC是⊙O的两条弦（即折线ABC是圆的一条折弦），BC>AB，M是的中点，则从M向BC所作垂线的垂足D是折弦ABC的中点，即CD=AB+BD．

    下面是运用“截长法”证明CD=AB+BD的部分证明过程．

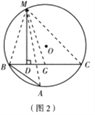
    证明：如图2，在CB上截取CG=AB，连接MA，MB，MC和MG．

    ∵M是的中点，

    ∴MA=MC

    任务：（1）请按照上面的证明思路，写出该证明的剩余部分；

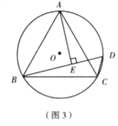
    （2）填空：如图（3），已知等边△ABC内接于⊙O，AB=2，D为⊙O上 一点, ，AE⊥BD与点E,则△BDC的周长是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某班50名学生期末考试数学成绩（单位：分）的频率分布直方图如图所示，其中数据不在分点上，对图中提供的信息作出如下的判断：

    ②成绩在79.5～89.5分段的人数占30%；
    ③成绩在79.5分以上的学生有20人；
    ④本次考试成绩的中位数落在69.5～79.5分段内．
    其中正确的判断有（ ）
    A.4个
    B.3个
    C.2个
    D.1个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的一元二次方程（a﹣1）x2+a2﹣1=0有一个根为0，则a=

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】因式分解：12a2b(x-y)-4ab(y-x).

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某年级组织学生参加夏令营，分为甲、乙、丙三组进行活动．下面两幅统计图反映了学生报名参加夏令营的情况．请你根据图中的信息回答下列问题：

    报名人数分布直方图 报名人数扇形统计图
    （1）求该年级报名参加本次活动的总人数；
    （2）求该年级报名参加乙组的人数，并补全频数分布直方图；
    （3）根据实际情况，需从甲组抽调部分同学到丙组，使丙组人数是甲组人数的3倍，那么，应从甲组抽调多少名学生到丙组？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的．下面是一个案例．
    原题：如图①，点 分别在正方形 的边 上， ，连接 ，则 ，试说明理由．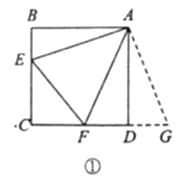

    （1）思路梳理
    因为 ，所以把 绕点 逆时针旋转90°至 ，可使 与 重合．因为 ，所以 ，点 共线．
    根据 ， 易证 ， 得 .请证明．
    （2）类比引申
    如图②，四边形 中， ， ，点 分别在边 上， .若 都不是直角，则当 与 满足等量关系时， 仍然成立，请证明．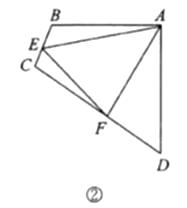

    （3）联想拓展
    如图③，在 中， ，点 均在边 上，且 .猜想 应满足的等量关系，并写出证明过程．

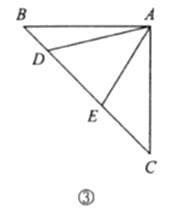
    查看答案和解析>>

    同步练习册答案