
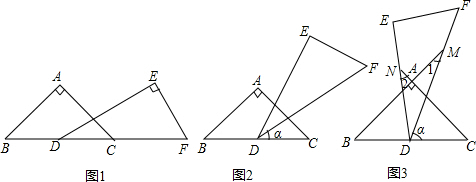
分析 (1)当∠EDC=∠B=45°时,DE∥AB,根据平行线的性质得30°+α=45°,解得α=15°;当DE∥AC时,DE⊥AB,根据平行线的性质得30°+α+45°=180°,解得α=105°;
(2)①连结MN,如图3,在△AMN中,由三角形内角和定理得∠ANM+∠AMN+∠MAN=180°,则∠ANM+∠AMN=90°,再在△MND中,利用三角形内角和定理得到∠2+∠ANM+∠AMN+∠1+∠MDN=180°,所以∠1+∠2=60°;
②根据∠1与∠2的关系列方程组$\left\{\begin{array}{l}{∠1+∠2=60°}\\{∠1=2∠2}\end{array}\right.$,然后解方程组即可;再根据三角形内角和定理和对顶角相等得到∠C+∠MDC=∠1+∠MAC,即45°+α=40°+90°,解得α=85°;
③由∠1≥$\frac{2}{3}$∠2,∠1+∠2=60°可解得∠1≥24°,由于∠C+∠MDC=∠1+∠MAC,即45°+α=∠1+90°,则∠1=α-45°,所以α-45°≥24°,解得α≥69°,利用直角三角板DEF的边DF、DE分别交BA、CA的延长线于点M、N得到α<90°,于是得到69°≤α<90°.
解答 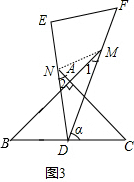 解:(1)∵∠B=45°,
解:(1)∵∠B=45°,
∴当∠EDC=∠B=45°时,DE∥AB,
而∠EDF=30°,
∴30°+α=45°,解得α=15°;
当DE∥AC时,DE⊥AB,
此时∠C+∠EDC=180°,
∴30°+α+45°=180°,解得α=105°;
故答案为15°,105°;
(2)①∠1与∠2度数的和不变.
连结MN,如图3,
在△AMN中,∵∠ANM+∠AMN+∠MAN=180°,
∴∠ANM+∠AMN=90°,
在△MND中,∵∠DNM+∠DMN+∠MDN=180°,
即∠2+∠ANM+∠AMN+∠1+∠MDN=180°,
∴∠1+∠2=180°-90°-30°=60°;
②根据题意得$\left\{\begin{array}{l}{∠1+∠2=60°}\\{∠1=2∠2}\end{array}\right.$,解得$\left\{\begin{array}{l}{∠1=40°}\\{∠2=20°}\end{array}\right.$;
∵∠C+∠MDC=∠1+∠MAC,
即45°+α=40°+90°,
∴α=85°;
③∵∠1≥$\frac{2}{3}$∠2,∠1+∠2=60°,
∴∠1≥$\frac{2}{3}$(60°-∠1),
∴∠1≥24°,
∵∠C+∠MDC=∠1+∠MAC,
即45°+α=∠1+90°,
∴∠1=α-45°,
∴α-45°≥24°,解得α≥69°,
∴∠α的度数范围为69°≤α<90°.
点评 本题考查了三角形内角和定理:三角形内角和是180°.也考查了解二元一次方程组.合理选择三角形后利用三角形内角和定理列等量关系是解决问题的关键,同时运用不等式的性质解决∠α的度数范围.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
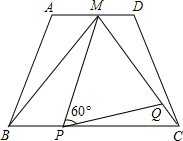 如图,在四边形ABCD中,AD∥BC,点M是AD的中点,AD=2,BC=4,△MBC是等边三角形.
如图,在四边形ABCD中,AD∥BC,点M是AD的中点,AD=2,BC=4,△MBC是等边三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -3x3y2z的系数是3 | B. | x2+x3是5次多项式 | ||
| C. | $\frac{1}{{x}^{2}}$不是整式 | D. | πr2是3次单项式 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com