
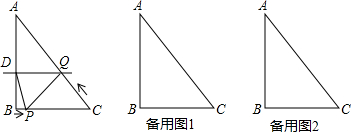
分析 (1)由在△ABC中,∠B=90°,AB=8,BC=6,利用勾股定理即可求得AC的长,继而求得sinA的值;
(2)由题意可得:QC=2t,即可得AQ=10-2t,由QD∥BC,可得△ADQ∽△ABC,然后由相似三角形的对应边成比例,用含有t的代数式表示DQ的长;
(3)首先作QE⊥BC于E,则可证得△CQE∽△CAB,然后由相似三角形的对应边成比例,表示出QE的长,即可表示出DB,又由△DPQ为直角三角形即∠DPQ=90°,可证得△PDB∽△DQP,求得DP2=$\frac{30t-6{t}^{2}}{5}$,在Rt△BPD中,由勾股定理得:BP2+BD2=DP2,即可求得t的值;
(4)由DQ∥BC,可得△DQE∽△OPE,然后由相似三角形的对应边成比例,求得DE,继而求得DO,然后由在Rt△BOD中,由勾股定理得:BD2+BO2=DO2,可得($\frac{8t}{5}$)2+($\frac{6+t}{2}$)2=($\frac{90-17t}{10}$)2,继而求得答案.
解答 解:(1)∵在△ABC中,∠B=90°,AB=8,BC=6,
∴AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=10,
∴sinA=$\frac{BC}{AC}$=$\frac{3}{5}$;
(2)当运动t秒时,QC=2t,
∴AQ=10-2t,
∵QD∥BC,
∴△ADQ∽△ABC,
∴DQ:BC=AQ:AC,
∴$\frac{DQ}{6}=\frac{10-2t}{10}$,
∴DQ=$\frac{30-6t}{5}$;
(3)存在.
如图1,作QE⊥BC于E,
则QE∥AB,
∴△CQE∽△CAB,
∴QE:AB=CQ:AC,
∴$\frac{QE}{8}=\frac{2t}{10}$,
∴QE=$\frac{8}{5}$t,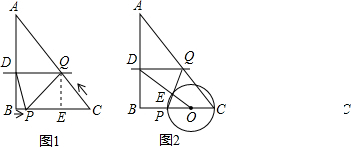 ∴DB=QE=$\frac{8}{5}$t,
∴DB=QE=$\frac{8}{5}$t,
∵△DPQ为直角三角形即∠DPQ=90°,
∴∠PDQ+∠PQD=90°,
∵∠PDB+∠PDQ=90°,
∴∠PQD=∠PDB,
∴△PDB∽△DQP,
∴BP:DP=DP:DQ,
∴$\frac{t}{DP}=\frac{DP}{\frac{30-6t}{5}}$,
∴DP2=$\frac{30t-6{t}^{2}}{5}$,
在Rt△BPD中,由勾股定理得:BP2+BD2=DP2,
∴t2+($\frac{8t}{5}$)2=$\frac{30t-6{t}^{2}}{5}$,
解得:t=$\frac{150}{119}$;
当∠DQP=90°时,BP=t,CQ=2t,QP=$\frac{8}{5}$t,
由CE2+QP2=CQ2,
解得t=$\frac{30}{11}$;
(4)如图2,当线段DO交PQ于点E且点E恰好落在⊙O上,
∵DQ∥BC,
∴△DQE∽△OPE,
∴PO:DQ=OE:DE,
∵OP=OE=$\frac{6-t}{2}$,
∴DE=DQ=$\frac{30-6t}{5}$,
∴DO=DE+OE=$\frac{90-17t}{10}$,
在Rt△BOD中,由勾股定理得:BD2+BO2=DO2,
∴($\frac{8t}{5}$)2+($\frac{6+t}{2}$)2=($\frac{90-17t}{10}$)2,
解得:t1=210+120$\sqrt{3}$(不符合题意),t2=210-120$\sqrt{3}$.
∴当线段DO交PQ于点E且点E恰好落在⊙O上时,t=210-120$\sqrt{3}$.
点评 此题属于圆的综合题,考查了相似三角形的判定与性质、勾股定理、圆周角定理以及三角函数等知识.注意掌握方程思想的应用是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放在平面直角坐标系中,
正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图所示的方式放在平面直角坐标系中,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a-$\frac{1}{2}$b)2=a2-$\frac{1}{2}$ab+$\frac{1}{4}$b2 | B. | -2a2($\frac{1}{2}$ab+b2)=-a3b+b2a2 | ||
| C. | -$\frac{1}{2}$a2bn•(3anbn+1)=-$\frac{3}{2}$a2nb${\;}^{{n}^{2}+n}$ | D. | (a-b)(-a-2b)=-a2-ab+2b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
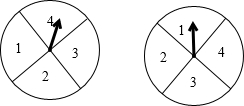 让图中两个转盘分别自由转动一次,当转盘停止转动时,两个指针分别落在某两个数所表示的区域,则这两个数的和概率最大的和等于( )
让图中两个转盘分别自由转动一次,当转盘停止转动时,两个指针分别落在某两个数所表示的区域,则这两个数的和概率最大的和等于( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com