
【题目】某花卉种植基地欲购进甲、乙两种君子兰进行培育,若购进甲种2株,乙种3株,则共需成本1700元 ;若购进甲种3株,乙种1株,则共需成本1500元,
(1)求甲乙两种君子兰每株成本多少元?
(2)该种植基地决定在成本不超过30000元的前提下购进甲乙两种君子兰,若购进乙种君子兰的株数比甲种君子兰的3倍还多10株,求最多购进甲种君子兰多少株?
【答案】(1)甲种君子兰每株成本为400元,乙种君子兰每株成本为300元;
(2)最多购进甲种君子兰20株.
【解析】试题分析:(1)设甲种君子兰每株成本为x元,乙种君子兰每株成本为y元.此问中的等量关系:①购进甲种2株,乙种3株,则共需要成本1700元;②购进甲种3株,乙种1株,则共需要成本1500元;依此列出方程求解即可;(2)结合(1)中求得的结果,根据题目中的不等关系:成本不超过30000元;列不等式进行分析.
试题解析:(1)设甲种君子兰每株成本为x元,乙种君子兰每株成本为y元,依题意有
![]() ,
,
解得![]() .
.
故甲种君子兰每株成本为400元,乙种君子兰每株成本为300元。
(2)设购进甲种君子兰a株,则购进乙种君子兰(3a+10)株,依题意有
400a+300(3a+10)30000,
解得a27013.
∵a为整数,
∴a最大为20.
故最多购进甲种君子兰20株。


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某企业生产并销售某种产品,假设销售量与产量相等,如图中的折线ABD、线段CD分别表示该产品每千克生产成本y1(单位:元)、销售价y2(单位:元)与产量x(单位:kg)之间的函数关系.
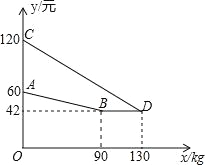
(1)求线段AB所表示的y1与x之间的函数表达式;线段CD所表示的y2与x之间的函数表达式.
(2)当该产品产量为多少时,获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,设点P(x1,y1),Q(x2,y2)是图形W上的任意两点.
定义图形W的测度面积:若|x1﹣x2|的最大值为m,|y1﹣y2|的最大值为n,则S=mn为图形W的测度面积.
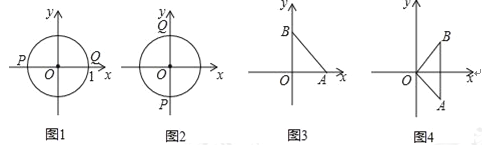
例如,若图形W是半径为1的⊙O,当P,Q分别是⊙O与x轴的交点时,如图1,|x1﹣x2|取得最大值,且最大值m=2;当P,Q分别是⊙O与y轴的交点时,如图2,|y1﹣y2|取得最大值,且最大值n=2.则图形W的测度面积S=mn=4
(1)若图形W是等腰直角三角形ABO,OA=OB=1.
①如图3,当点A,B在坐标轴上时,它的测度面积S= ;
②如图4,当AB⊥x轴时,它的测度面积S= ;
(2)若图形W是一个边长1的正方形ABCD,则此图形的测度面积S的最大值为 ;
(3)若图形W是一个边长分别为3和4的矩形ABCD,求它的测度面积S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
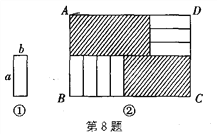
【题目】将7张如图①所示的长为a、宽为b(a>b)的小长方形纸片,按如图②所示的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示,设左上角与右下角的阴影部分的面积之差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a、b应满足( )
A. a=![]() b B. a=3b C. a=
b B. a=3b C. a=![]() b D. a=4b
b D. a=4b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读材料,再解答下列问题:
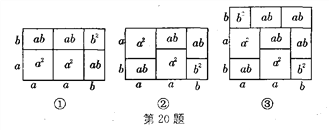
我们已经知道,多项式与多项式相乘的法则可以用平面几何图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示.例如:(2a+b) (a+b)=2a2+3ab+b2就可以用图①或图②等图形的面积来表示.
(1)请写出图③所表示的代数恒等式:
(2)画出一个几何图形,使它的面积能表示(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.
(3)请仿照上述方法写出另一个含a、b的代数恒等式,并画出与之对应的几何图形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com