
����Ŀ����ƽ��ֱ������ϵxOy�У����P��x1��y1����Q��x2��y2����ͼ��W�ϵ��������㣮
����ͼ��W�IJ���������|x1��x2|�����ֵΪm��|y1��y2|�����ֵΪn����S=mnΪͼ��W�IJ�������
���磬��ͼ��W�ǰ뾶Ϊ1�ġ�O����P��Q�ֱ��ǡ�O��x��Ľ���ʱ����ͼ1��|x1��x2|ȡ�����ֵ�������ֵm=2����P��Q�ֱ��ǡ�O��y��Ľ���ʱ����ͼ2��|y1��y2|ȡ�����ֵ�������ֵn=2����ͼ��W�IJ�����S=mn=4
��1����ͼ��W�ǵ���ֱ��������ABO��OA=OB=1��
����ͼ3������A��B����������ʱ�����IJ�����S= ��
����ͼ4����AB��x��ʱ�����IJ�����S= ��
��2����ͼ��W��һ���߳�1��������ABCD�����ͼ�εIJ�����S�����ֵΪ ��
��3����ͼ��W��һ���߳��ֱ�Ϊ3��4�ľ���ABCD�������IJ�����S��ȡֵ��Χ��
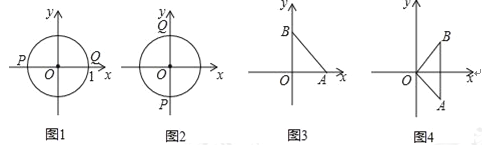
���𰸡���1��1,1����2��2����3��12��S��![]() ��
��
��������
�����������1���ɲ������Ķ����������IJ�����S=|OA||OB|��⼴�ɣ�
�����õ���ֱ�������ε��������AC��AB�����ò�����S=|AB||OC|��⼴�ɣ�
��2����ȷ������������������Sʱ��ͼ�Σ��������ò�����S=|AC||BD|��⣮
��3�������������A��B��B��C����x����ʱ��������A��C������x����ʱ�ֱ���⼴�ɣ�
�����������1������ͼ3��
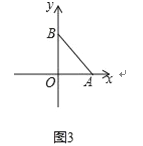
��OA=OB=1����A��B���������ϣ�
�����IJ�����S=|OA||OB|=1��
�ʴ�Ϊ��1��
����ͼ4��
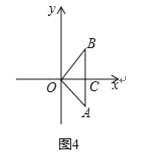
��AB��x�ᣬOA=OB=1��
��AB=![]() ��OC=
��OC=![]() ��
��
�����IJ�����S=|AB||OC|=![]() ��
��![]() =1��
=1��
�ʴ�Ϊ��1��
��2����ͼ5��ͼ�εIJ�����S��ֵ���
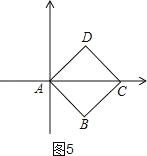
���ı���ABCD�DZ߳�Ϊ1�������Σ�
�����IJ�����S=|AC||BD|=![]() ��
��![]() =2��
=2��
�ʴ�Ϊ��2��
��3�������ABCD�ı�AB=4��BC=3������֪�ɵã�ƽ��ͼ��W����ı���������Ĵ�С��������ABCD������һ������Bƽ����x���ϣ�
��A��B��B��C����x����ʱ��
��ͼ6��ͼ7��
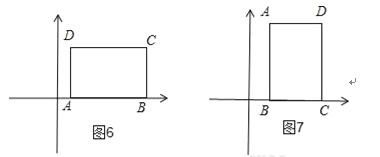
����ABCD�IJ�����S���Ǿ���ABCD���������ʱS=12��
������A��C������x����ʱ����ͼ8������A��ֱ��AH��x���ڵ�E����C����CF��x���ڵ�F������D��ֱ��GH��x�ᣬ�ֱ�AE��CF�ڵ�H��G����ɵ��ı���EFGH�Ǿ��Σ�
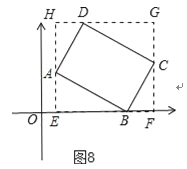
����P��Q���A��C�غ�ʱ��|x1��x2|�����ֵΪm=EF��|y1��y2|�����ֵΪn=GF��
ͼ��W�IJ�����S=EFGF��
�ߡ�ABC+��CBF=90�㣬��ABC+��BAE=90�㣬
���CBF=��BAE��
�ߡ�AEB=��BFC=90�㣬
���AEB�ס�BFC��
��![]() ��
��
��AE=4a��EB=4b����a��0��b��0������BF=3a��FC=3b��
��RT��AEB��AE2+BE2=AB2��
��16a2+16b2=16����a2+b2=1��
��b��0��
��![]() ��
��
�ڡ�ABE�͡�CDG�У�
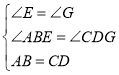
���ABE�ա�CDG��AAS��
��CG=AE=4a��
��EF=EB+BF=4b+3a��GF=FC+CG=3b+4a��
��ͼ��W�IJ�����S=EFGF=��4b+3a����3b+4a��
=12a2+12b2+25a![]() =12+25
=12+25![]() =12+25
=12+25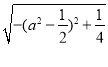 ��
��
��![]() ʱ����a=
ʱ����a=![]() ʱ��������Sȡ�����ֵ12+25��
ʱ��������Sȡ�����ֵ12+25��![]() =
=![]() ��
��
��a��0��b��0��
��![]() ��
��
��S��12��
����������������S��ȡֵ��ΧΪ12��S��![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ�����ľ���ֵ����������̵�����1����������ǣ� ��
A.���� B.����C.���� D.�Ǹ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ�ž���ֽƬABCD����ͼ��ʽ�۵���ʹ����B���ڱ�AD�ϣ���Ϊ��B��������A���ڵ�A�������ۺ۷ֱ����AD��BC���ڵ�E��F��
��1������ͼ������BE����֤���ı���BFB��E�����Σ�
��2����AB��8��BC��16�����߶�BF����ȡ��������ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ե�Բ�ܽǵĶ�����36���������������Ե�Բ�ĽǵĶ����ǣ�������
A. 72�� B. 54�� C. 36�� D. 18��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ���У�������Գ�ͼ���������ĶԳ�ͼ�ε��ǣ� ��
A. �ȱ�������B. ����
C. ����ֱ��������D. ƽ���ı���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У����û�����ʵ������֮�䣬�߶�����������͵������ǣ� ��
A. ���������ӾͿ���ľ���̶���ǽ��
B. �������Ĺ�·��ֱ����������·��
C. ����Բ����ԱȽ������߶εĴ�С��ϵ
D. ֲ��ʱ��ֻҪ������������λ�ã�����ȷ��ͬһ�������ڵ�ֱ�ߡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij������ֲ�����������ס������־�������������������������2�꣬����3�꣬����ɱ�1700Ԫ ������������3�꣬����1�꣬����ɱ�1500Ԫ��
��1����������־�����ÿ��ɱ�����Ԫ��
��2������ֲ���ؾ����ڳɱ�������30000Ԫ��ǰ���¹����������־����������������־������������ȼ��־�������3������10�꣬���������־����������ꣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����a��3��b��Ϊ2(a��3)��5��2b��5������������õ�ʽ�����ʼ�˳����( )
A. ���õ�ʽ������1�����õ�ʽ������2
B. ���õ�ʽ������2�����õ�ʽ������1
C. �����˵�ʽ������1
D. �����˵�ʽ������2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com