
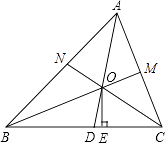
【题目】如图,在△ABC中,三个内角的平分线AD、BM、CN交于点O,OE⊥BC于点E.
(1)求∠ABO+∠BCO+∠CAO的度数;
(2)∠BOD与∠COE是否相等?请说明理由.
【答案】
(1)解:∵AD、BM、CN是△ABC三个内角的平分线,
∴∠BAO=∠CAO= ![]() ∠BAC,∠ABO=∠CBO=
∠BAC,∠ABO=∠CBO= ![]() ∠ABC,∠ACO=∠BCO=
∠ABC,∠ACO=∠BCO= ![]() ∠ACB,
∠ACB,
∴∠ABO+∠BCO+∠CAO= ![]() (∠ABC+∠ACB+∠BAC).
(∠ABC+∠ACB+∠BAC).
∵∠ABC+∠ACB+∠BAC=360°,
∴∠ABO+∠BCO+∠CAO=90°.
(2)解:∠BOD=∠COE,理由如下:
∵∠BOD是△ABO的外角,
∴∠BOD=∠ABO+∠BAO= ![]() (∠ABC+∠BAC)=
(∠ABC+∠BAC)= ![]() (180°﹣∠ACB)=90°﹣
(180°﹣∠ACB)=90°﹣ ![]() ∠ACB.
∠ACB.
∵OE⊥BC,
∴∠COE+∠BCO=90°,
∴∠COE=90°﹣∠BCO=90°﹣ ![]() ∠ACB.
∠ACB.
∴∠BOD=∠COE.
【解析】(1)根据角平分线的定义可得∠BAO=∠CAO=![]() ∠BAC、∠ABO=∠CBO=
∠BAC、∠ABO=∠CBO=![]() ∠ABC、∠ACO=∠BCO=
∠ABC、∠ACO=∠BCO=![]() ∠ACB,结合三角形的内角和可得∠ABO+∠BCO+∠CAO=
∠ACB,结合三角形的内角和可得∠ABO+∠BCO+∠CAO=![]() (∠ABC+∠ACB+∠BAC)=90°;
(∠ABC+∠ACB+∠BAC)=90°;
(2)根据三角形外角的性质可得∠BOD=∠ABO+∠BAO=90°-![]() ∠ACB,由OE⊥BC结合三角形内角和可得出∠COE=90°-∠BCO=90°-
∠ACB,由OE⊥BC结合三角形内角和可得出∠COE=90°-∠BCO=90°-![]() ∠ACB,进而可得出∠BOD=∠COE.
∠ACB,进而可得出∠BOD=∠COE.
【考点精析】解答此题的关键在于理解三角形的内角和外角的相关知识,掌握三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】我们将在直角坐标系中圆心坐标和半径均为整数的圆称为“整圆”.如图,直线l:![]() 与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
与x轴、y轴分别交于A、B,∠OAB=30°,点P在x轴上,⊙P与l相切,当P在线段OA上运动时,使得⊙P成为整圆的点P个数是( )
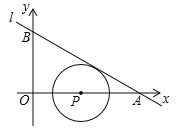
A.6 B.8 C.10 D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究:中华人民共和国国旗上的五角星的每个角均相等,小明为了计算每个角的度数,画出了如图①的五角星,每个角均相等,并写出了如下不完整的计算过程,请你将过程补充完整.
解:∵∠AFG=∠C+∠E,∠AGF=∠B+∠D.
∴∠AFG+∠AGF=∠C+∠E+∠B+∠D.
∵∠A+∠AFG+∠AGF=°,
∴∠A+∠B+∠C+∠D+∠E=°,
∴∠A=∠B=∠C=∠D=∠E=°.
拓展:如图②,小明改变了这个五角星的五个角的度数,使它们均不相等,请你帮助小明求∠A、∠B、∠C、∠D、∠E的和.
应用:如图③.小明将图②中的点A落在BE上,点C落在BD上,若∠B=∠D=36°,则∠CAD+∠ACE+∠E=°.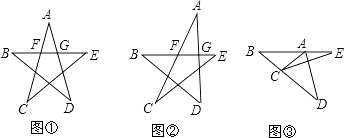
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校师生为了对学生零花钱的使用进行教育指导,对全班50名学生每人一周内的零花钱数额进行了调查统计,并绘制如下统计表:
零花钱数额/元 | 5 | 10 | 15 | 20 |
学生人数/名 | a | 15 | 20 | 5 |
根据表格中信息,回答下列问题:
(1)求a的值.
(2)求着50名学生每人一周内零花钱数额的中位数.
(3)随机抽查一名学生,抽到一周内零花钱数额不大于10元的同学概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,L是四边形ABCD的对称轴,如果AD∥BC,有下列结论:
(1)①AB∥CD;②AB=CD;③AB⊥BC;④AO=OC
其中正确的结论是(把你认为正确的结论的序号都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计结果如下表:
班级 | 参赛人数 | 中位数 | 方差 | 平均数 |
甲 | 55 | 149 | 191 | 135 |
乙 | 55 | 151 | 110 | 135 |
某同学分析上表后得出如下结论:
①甲、乙两班学生成绩平均水平相同;
②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字≥150个为优秀);
③甲班成绩的波动比乙班大,
上述结论正确的是( )
A.①②③
B.①②
C.①③
D.②③
查看答案和解析>>
科目:初中数学 来源: 题型:
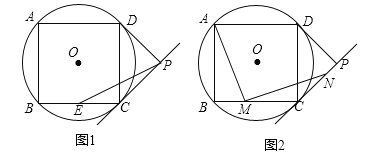
【题目】如图,四边形ABCD是⊙O的内接正方形,AB=4,PC、PD是⊙O的两条切线,C、D为切点.
(1)如图1,求⊙O的半径;
(2)如图1,若点E是BC的中点,连接PE,求PE的长度;
(3)如图2,若点M是BC边上任意一点(不含B、C),以点M为直角顶点,在BC的上方作∠AMN=90°,交直线CP于点N,求证:AM=MN.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下面是按照一定规律画出的“数形图”,经研究可以发现:图 ![]() 比图
比图 ![]() 多出2个“树枝”,图
多出2个“树枝”,图 ![]() 比图
比图 ![]() 多出4个“树枝”,图
多出4个“树枝”,图 ![]() 比图
比图 ![]() 多出8个“树枝”,照此规律,图
多出8个“树枝”,照此规律,图 ![]() 比图
比图 ![]() 多出个“树枝”.
多出个“树枝”.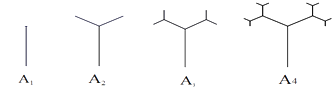
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com