
【题目】如图,L是四边形ABCD的对称轴,如果AD∥BC,有下列结论:
(1)①AB∥CD;②AB=CD;③AB⊥BC;④AO=OC
其中正确的结论是(把你认为正确的结论的序号都填上).
科目:初中数学 来源: 题型:
【题目】如图,将△ABC纸片的一角折叠,使点C落在△ABC内一点C′上,若∠1=30°,∠2=36°,则∠C的度数是( )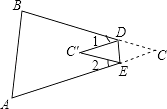
A.33°
B.34°
C.31°
D.32°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,三个内角的平分线AD、BM、CN交于点O,OE⊥BC于点E.
(1)求∠ABO+∠BCO+∠CAO的度数;
(2)∠BOD与∠COE是否相等?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据图中给出的信息,解答下列问题: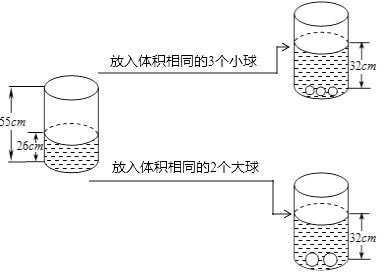
(1)放入一个小球水面升高cm,放入一个大球水面升高cm.
(2)放入大球、小球共10个,如果要使水面上升到50cm,求放入大球、小球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】供电局的电力维修工要到30千米远的郊区进行电力抢修.技术工人骑摩托车先走,15分钟后,抢修车装载着所需材料出发,结果他们同时到达.已知抢修车的速度是摩托车的1.5倍,求这两种车的速度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(操作发现】
在计算器上输入一个正数,不断地按“![]() ”键求算术平方根,运算结果越来越接近1或都等于1.
”键求算术平方根,运算结果越来越接近1或都等于1.
【提出问题】
输入一个实数,不断地进行“乘以常数k,再加上常数b”的运算,有什么规律?
【分析问题】
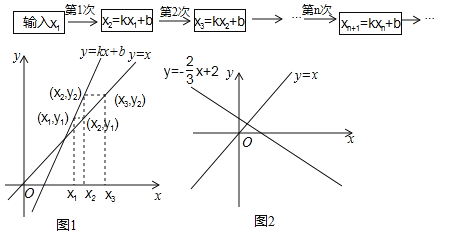
我们可用框图表示这种运算过程(如图a).
也可用图象描述:如图1,在x轴上表示出x1,先在直线y=kx+b上确定点(x1,y1),再在直线y=x上确定纵坐标为y1的点(x2,y1),然后再x轴上确定对应的数x2,…,以此类推.
【解决问题】
研究输入实数x1时,随着运算次数n的不断增加,运算结果x,怎样变化.
(1)若k=2,b=﹣4,得到什么结论?可以输入特殊的数如3,4,5进行观察研究;
(2)若k>1,又得到什么结论?请说明理由;
(3)①若![]() ,b=2,已在x轴上表示出x1(如图2所示),请在x轴上表示x2,x3,x4,并写出研究结论;
,b=2,已在x轴上表示出x1(如图2所示),请在x轴上表示x2,x3,x4,并写出研究结论;
②若输入实数x1时,运算结果xn互不相等,且越来越接近常数m,直接写出k的取值范围及m的值(用含k,b的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com