
【题目】已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过点A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.
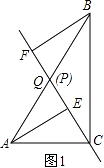
(1)当点P与点Q重合时,如图1,写出QE与QF的数量关系,不证明;
(2)当点P在线段AB上且不与点Q重合时,如图2,(1)的结论是否成立?并证明;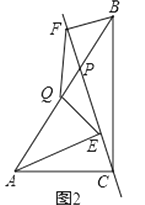
(3)当点P在线段BA(或AB)的延长线上时,如图3,此时(1)的结论是否成立?请画出图形并给予证明.
【答案】
(1)
解:QE=QF,
理由是:如图1,∵Q为AB中点,
∴AQ=BQ,
∵BF⊥CP,AE⊥CP,
∴∠BFQ=∠AEQ=90°,
在△BFQ和△AEQ中 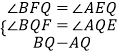
∴△BFQ≌△AEQ(AAS),
∴QE=QF,
(2)
解:中的结论仍然成立,
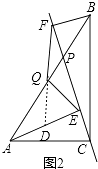
证明:如图2,延长FQ交AE于D,
∵Q为AB中点,
∴AQ=BQ,
∵BF⊥CP,AE⊥CP,
∴BF∥AE,
∴∠QAD=∠FBQ,
在△FBQ和△DAQ中, 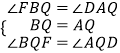 ,
,
∴△FBQ≌△DAQ(ASA),
∴QF=QD,
∵AE⊥CP,
∴EQ是Rt△DEF斜边上的中线,
∴QE=QF=QD,
即QE=QF.
(3)
解:(1)中的结论仍然成立,
证明:如图3,
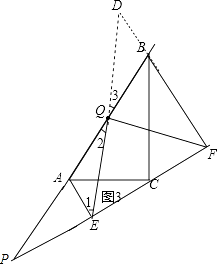
延长EQ、FB交于D,
∵Q为AB中点,
∴AQ=BQ,
∵BF⊥CP,AE⊥CP,
∴BF∥AE,
∴∠1=∠D,
在△AQE和△BQD中, 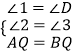 ,
,
∴△AQE≌△BQD(AAS),
∴QE=QD,
∵BF⊥CP,
∴FQ是Rt△DEF斜边DE上的中线,
∴QE=QF.
【解析】(1)证△BFQ≌△AEQ即可;(2)证△FBQ≌△DAQ,推出QF=QD,根据直角三角形斜边上中线性质求出即可;(3)证△AEQ≌△BDQ,推出DQ=QE,根据直角三角形斜边上中线性质求出即可
【考点精析】利用三角形的“三线”对题目进行判断即可得到答案,需要熟知1、三角形角平分线的三条角平分线交于一点(交点在三角形内部,是三角形内切圆的圆心,称为内心);2、三角形中线的三条中线线交于一点(交点在三角形内部,是三角形的几何中心,称为中心);3、三角形的高线是顶点到对边的距离;注意:三角形的中线和角平分线都在三角形内.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某中学为了绿化校园,计划购买一批榕树和香樟树,经市场调查,榕树的单价比香樟树少20元,购买3棵榕树和2棵香樟树共需340元.
(1)榕树和香樟树的单价各是多少?
(2)根据学校实际情况,需购买两种树苗共150棵,总费用不超过10840元,且购买香樟树的棵数不少于榕树的1.5倍,请你算算该校本次购买榕树和香樟树共有哪几种方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC为等边三角形,AB=2,点D为边AB上一点,过点D作DE∥AC,交BC于E点;过E点作EF⊥DE,交AB的延长线于F点.设AD=x,△DEF的面积为y,则能大致反映y与x函数关系的图象是( )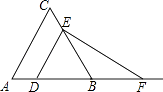
A.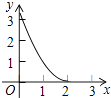
B.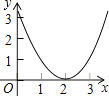
C.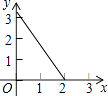
D.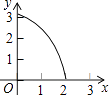
查看答案和解析>>
科目:初中数学 来源: 题型:
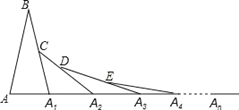
【题目】在第1个△ABA1中,∠B=20°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D;…,按此做法进行下去,第n个三角形的以An为顶点的内角的度数为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(5mn2﹣4m2n)(﹣2mn)
(2)(x+7)(x﹣6)﹣(x﹣2)(x+1)
(3) (-![]() )2 016×161 008;
)2 016×161 008;
【答案】(1)﹣10m2n3+8m3n2;(2)2x﹣40;(3)1.
【解析】试题分析:(1)原式利用单项式乘以多项式法则计算即可得到结果;
(2)原式两项利用多项式乘以多项式法则计算,去括号合并即可得到结果;
(3)先根据幂的乘方的逆运算,把(-![]() )2 016化为(
)2 016化为(![]() )1008,再根据积的乘方的逆运算计算即可.
)1008,再根据积的乘方的逆运算计算即可.
试题解析:(1)原式=(5mn2)(﹣2mn)+(﹣4m2n)(﹣2mn)=﹣10m2n3+8m3n2;
(2)原式=x2﹣6x+7x﹣42﹣x2﹣x+2x+2=2x﹣40.
(3)原式=(![]() )1008×161 008=(
)1008×161 008=(![]() ×16)1 008=1.
×16)1 008=1.
【题型】解答题
【结束】
19
【题目】如图,方格图中每个小正方形的边长为1,点A、B、C都是格点.
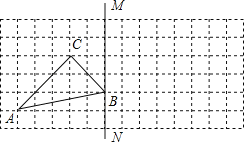
(1)画出△ABC关于直线BM对称的△A1B1C1;
(2)写出AA1的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC底边BC的长为4cm,面积是12cm2,腰AB的垂直平分线EF交AC于点F,若D为BC边上的中点,M为线段EF上一动点,则△BDM的周长最短为______cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队(有甲、乙两组)承包一项工程,规定若干天内完成.
①已知甲组单独完成这项工程所需时间比规定时间多30天,乙组单独完成这项工程所需时间比规定时间多12天,如果甲乙两组先合做20天,剩下的由甲组单独做,恰好按规定的时间完成,那么规定的时间是多少天?
②实际工作中,甲乙两组合做完成这项工程的![]() 后,工程队又承包了新工程,需要抽调一组过去,从按时完成任务考虑,你认为留下哪一组更好?说明理由.
后,工程队又承包了新工程,需要抽调一组过去,从按时完成任务考虑,你认为留下哪一组更好?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,若干个半径为2个单位长度,圆心角为60°的扇形组成一条连续的曲线,点P从原点O出发,沿这条曲线向右上下起伏运动,点在直线上的速度为2个单位长度/秒,点在弧线上的速度为 ![]() 个单位长度/秒,则2017秒时,点P的坐标是( )
个单位长度/秒,则2017秒时,点P的坐标是( ) 
A.(2017,0)
B.(2017, ![]() )
)
C.(2017,﹣ ![]() )
)
D.(2016,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com