
分析 (1)由“应付美元数=报价人民币数×美元对人民币的汇率”,套入数据即可得出结论;
(2)根据“人民币升值后的汇率=升值前的汇率×(1+升值百分比)”,套入数据即可得出结论;
(3)由“人民币钱数=实付美元数÷美元对人民币的汇率”,算出折合人民币数,再除以b即可得出结论;
(4)设人民币平均每月升值x%,由“两个月前汇率÷(1+每月升值百分数)的平方的商=当前月汇率”得出关于x的分式方程,解方程即可求出人民币平均每月升值百分数,再结合该升值百分数算出两个月后的美元的汇率,套入“应付美元数=报价人民币数×美元对人民币的汇率”即可得出结论.
解答 解:(1)b•$\frac{1}{a}$=$\frac{b}{a}$(万美元),
答:该企业这一单出口产品按汇率1:a报美元价为$\frac{b}{a}$万美元.
(2)1:$\frac{a}{1+1%}$=100:101a.
答:经30天后与外商结算时,美元对人民币的汇率为100:101a.
(3)$\frac{b}{a}$•$\frac{100}{101}$•a=$\frac{100}{101}$b(万元),
1-($\frac{100}{101}$b÷b)×100%≈0.99%.
答:外商按所报的美元价付钱,根据当时美元对人民币的汇率,折合人民币$\frac{100}{101}$b万元,比报价约减少了0.99%.
(4)设人民币平均每月升值x%,
根据已知得:$\frac{6.6}{(1+x%)^{2}}$=6.46,
解得:x≈1,或x≈-201(舍去).
200÷$\frac{6.46}{(1+1%)^{2}}$≈31.58(万美元).
答:人民币平均每月升值约1%,为了避免因人民币升值带来的经济损失,我认为这单出口产品需报价约31.58万美元(精确到0.01万美元).
点评 本题考查了一元二次方程的应用、解分式方程以及比例的应用,解题的关键是结合数量关系列出算式(或方程).本题属于基础题,难度不大,但在解题过程中要时刻牢记比的应用,莫要颠倒了顺序.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
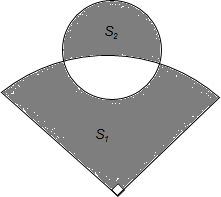 如图,在半径为5,圆心角为90°的扇形中,阴影部分的面积S1;在半径为2的圆中,阴影部分的面积为S2,则S1-S2=$\frac{9}{4}$π(结果保留π).
如图,在半径为5,圆心角为90°的扇形中,阴影部分的面积S1;在半径为2的圆中,阴影部分的面积为S2,则S1-S2=$\frac{9}{4}$π(结果保留π).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在边长为1的小正方形网格中,△AOB的顶点均在格点上,
在边长为1的小正方形网格中,△AOB的顶点均在格点上,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD是平行四边形,AD=30cm,AB=20cm,∠D=60°,E、F分别为AB和CD边上的两个动点,E从A向B运动,F从D向C运动,若点E的速度是1cm/秒,点F的速度是2cm/秒.
如图,四边形ABCD是平行四边形,AD=30cm,AB=20cm,∠D=60°,E、F分别为AB和CD边上的两个动点,E从A向B运动,F从D向C运动,若点E的速度是1cm/秒,点F的速度是2cm/秒.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
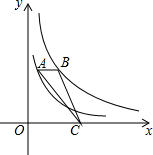 如图,点A在双曲线y=$\frac{2}{x}$上,点B在双AB曲线y=$\frac{5}{x}$上.点C是x轴上一动点.若AB∥x轴.则△ABC的面积为1.5.
如图,点A在双曲线y=$\frac{2}{x}$上,点B在双AB曲线y=$\frac{5}{x}$上.点C是x轴上一动点.若AB∥x轴.则△ABC的面积为1.5.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
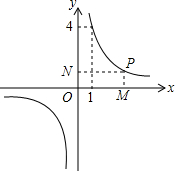 如图所示,P是反比例函数y=$\frac{k}{x}$的图象上任意一点,过点P分别作x轴、y轴的垂线,垂足分别为M,N.
如图所示,P是反比例函数y=$\frac{k}{x}$的图象上任意一点,过点P分别作x轴、y轴的垂线,垂足分别为M,N.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
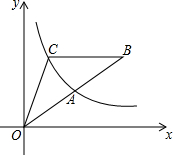 如图,点A是反比例函数y=$\frac{k}{x}$的图象上的一点,B是直线OA上的一点,且OA=AB,过点B作x轴的平行线交曲线y=$\frac{k}{x}$于点C,连OC,若S△ABC=9,那么k的值等于6.
如图,点A是反比例函数y=$\frac{k}{x}$的图象上的一点,B是直线OA上的一点,且OA=AB,过点B作x轴的平行线交曲线y=$\frac{k}{x}$于点C,连OC,若S△ABC=9,那么k的值等于6.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com