
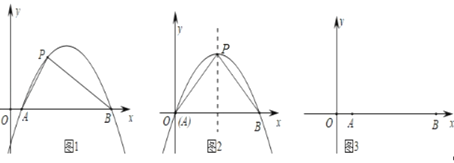
����Ŀ����ͼ1��������y��ax2+bx+c(a��0)��x�ύ��A��B���㣬��P����������(��A��B���㲻�غ�)������ABP����������AP2+BP2��AB2�������dzƵ�PΪ������y��ax2+bx+c(a��0)�Ĺ��ɵ㣮
(1)ֱ��д��������y��x2��1�Ĺ��ɵ�����Ϊ_____��
(2)��ͼ2����֪�����ߣ�y��ax2+bx(a��0��b��0)��x�ύ��A��B���㣬��PΪ�����ߵĶ��㣬�ʵ�P�ܷ�Ϊ�����ߵĹ��ɵ㣬���ܣ����b��ֵ��
(3)��ͼ3����ƽ��ֱ������ϵ�У���A(2��0)��B(12��0)����P��x��ľ���Ϊ1����P�ǹ�A��B������������ϵĹ��ɵ㣬���P��A��B����������ߵĽ���ʽ�͵�P�����꣮
���𰸡�(1)(0����1)��(2)��b��2ʱ����PΪ�����ߵĹ��ɵ㣻(3)����P��A��B����������ߵĽ���ʽΪy����x2+14x��24ʱ����P������Ϊ(7��2![]() ��1)��(7+2
��1)��(7+2![]() ��1)������P��A��B����������ߵĽ���ʽΪy��x2��14x+24ʱ����P������Ϊ(7��2
��1)������P��A��B����������ߵĽ���ʽΪy��x2��14x+24ʱ����P������Ϊ(7��2![]() ����1)��(7+2
����1)��(7+2![]() ����1)��
����1)��
��������
��1������������![]() ��֪��
��֪��![]() ��Ľ������꼰
��Ľ������꼰![]() �ij��ȣ��蹴�ɵ������Ϊ
�ij��ȣ��蹴�ɵ������Ϊ![]() ���ٸ��ݹ��ɵ�Ķ����������ɵ�����ꣻ
���ٸ��ݹ��ɵ�Ķ����������ɵ�����ꣻ
��2�������䷽���������![]() �����꣬�ɵ�
�����꣬�ɵ�![]() Ϊ�����ߵĹ��ɵ��֪
Ϊ�����ߵĹ��ɵ��֪![]() Ϊ����ֱ�������Σ����õ���ֱ�������ε����ʼ������
Ϊ����ֱ�������Σ����õ���ֱ�������ε����ʼ������![]() ��ֵ��
��ֵ��
��3�����![]() ������Ϊ
������Ϊ![]() ����
����![]() ��
��![]() ��ľ���Ϊ1��֪
��ľ���Ϊ1��֪![]() �����ݹ��ɵ�Ķ�����г�����
�����ݹ��ɵ�Ķ�����г�����![]() ��һԪ���η��̣����ɵó���
��һԪ���η��̣����ɵó���![]() �����꣬�ɵ�
�����꣬�ɵ�![]() ������������ߵĽ���ʽΪ
������������ߵĽ���ʽΪ![]() ����
����![]() ����������ϵ��������������������ߵĽ���ʽ.
����������ϵ��������������������ߵĽ���ʽ.
�⣺(1)��![]() ʱ��
ʱ��![]() ��
��
��֮�ã�![]() ��
��
���A������Ϊ![]() ����B������Ϊ
����B������Ϊ![]() ��
��![]() ��
��
��������![]() �Ĺ��ɵ�����Ϊ
�Ĺ��ɵ�����Ϊ![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��ã�![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
��ã�![]() ��
��
��������![]() �Ĺ��ɵ�����Ϊ
�Ĺ��ɵ�����Ϊ![]() ��
��
�ʴ�Ϊ��![]() ��
��
(2)��![]() ��
��
���P������Ϊ![]() ��
��
����P��Ϊ�����ߵĹ��ɵ㣬��![]() Ϊ����ֱ�������Σ�
Ϊ����ֱ�������Σ�
��![]() ��
��
��![]() ��
��
�൱![]() ʱ����PΪ�����ߵĹ��ɵ㣮
ʱ����PΪ�����ߵĹ��ɵ㣮
(3)���P������Ϊ![]() ��
��
�ߵ�P��x��ľ���Ϊ1��
��![]() ��
��
��![]() ����A������Ϊ
����A������Ϊ![]() ����B������Ϊ
����B������Ϊ![]() ��
��
��������֮��ľ��빫ʽ
��![]() ��
��
��![]() ��
��
��ã�![]() ��
��
���P������Ϊ![]() ����
����
���P��A��B����������ߵĽ���ʽΪ![]() ��
��
����P������Ϊ![]() ʱ����
ʱ����![]() ����
����![]() ����֮�ã�
����֮�ã�
![]() ��
��
�����P��A��B����������ߵĽ���ʽΪ![]() ����
����![]() ��
��
ͬ��������P������Ϊ![]() ʱ����P��A��B����������ߵĽ���ʽΪ
ʱ����P��A��B����������ߵĽ���ʽΪ![]() ��
��
����P������Ϊ![]() ʱ����P��A��B����������ߵĽ���ʽΪ
ʱ����P��A��B����������ߵĽ���ʽΪ![]() ��
��
����P������Ϊ![]() ʱ����P��A��B����������ߵĽ���ʽΪ
ʱ����P��A��B����������ߵĽ���ʽΪ![]() ��
��
��������������P��A��B����������ߵĽ���ʽΪ![]() ʱ����P������Ϊ
ʱ����P������Ϊ![]() ��
��![]() ��
��
����P��A��B����������ߵĽ���ʽΪ![]() ʱ����P������Ϊ
ʱ����P������Ϊ![]() ��
��![]() ��
��


 �����ܿ����ϵ�д�
�����ܿ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУΪ���ư�ѧ�������ƻ��ɹ�A��B�����ͺŵĿյ�����֪�ɹ�3̨A�Ϳյ���2̨B�Ϳյ��������39000Ԫ��4̨A�Ϳյ���5̨B�Ϳյ��ķ��ö�6000Ԫ��
��1����A�Ϳյ���B�Ϳյ�ÿ̨�������Ԫ��
��2����ѧУ�ƻ��ɹ�A��B�����ͺſյ���30̨����A�Ϳյ���̨��������B�Ϳյ���һ�룬�����ͺſյ��IJɹ��ܷ��ò�����217000Ԫ����У�����ļ��ֲɹ�������
��3���ڣ�2���������£�������һ�ֲɹ�������ʹ�ܷ�����ͣ���ͷ����Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
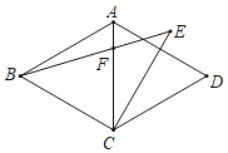
����Ŀ����ͼ��������ABCD�У���BAD��120�㣬CE��AD����CE��BC������BE���Խ���AC�ڵ�F�����EFC��_____�㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����|m+3|+![]() ��0����P��m��n������x��ĶԳƵ�P��Ϊ���κ���ͼ�㣬����κ����Ľ���ʽΪ��������
��0����P��m��n������x��ĶԳƵ�P��Ϊ���κ���ͼ�㣬����κ����Ľ���ʽΪ��������
A. y��![]() ��x��3��2+2B. y��
��x��3��2+2B. y��![]() ��x+3��2��2
��x+3��2��2
C. y��![]() ��x��3��2��2D. y��
��x��3��2��2D. y��![]() ��x+3��2+2
��x+3��2+2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
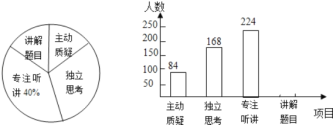
����Ŀ������ɫ�ɼ����ж�һ�����еľ��꼶ѧ�����Ծ��������ϲ���ѧϰ��������Ƚ��е��飬������Ŀ��Ϊ�������ɡ�����˼����רע������������Ŀ��������������ȡ�����������꼶ѧ���IJ������������������������������ͳ��ͼ�������ͼ��������Ϣ����������⣺
(1)����������У�һ�������_____��ѧ����
(2)�뽫����ͼ����������
(3)���ȫ����5200�����꼶ѧ������ô���Ծ��������У�������˼�����ľ��꼶ѧ���ж�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ABC��ֱ������ƽ���ڣ��������������ֱ�ΪA��0��3����B��3��4����C��2��2����������������ÿ��С�����εı߳���һ����λ���ȣ���
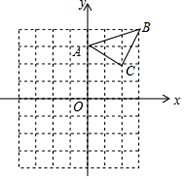
��1����ABC����ƽ��4����λ���ȵõ�����A1B1C1����C1�������� ��
��2���Ե�BΪλ�����ģ��������ڻ�����A2B2C2��ʹ��A2B2C2����ABCλ�ƣ���λ�Ʊ�Ϊ2��1����C2�������� ��������ͼ�Σ�
��3����A2B2C2������� ƽ����λ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���Ӽҳ��������������ڹ�����һ��ʱ���ԭ·���أ�ͬʱС���ְִӹ���С����·�߷��ؼ��У���ͼ��������ҵľ���y���ף���С��������ʱ��x���֣�֮��ĺ���ͼ�������н����в���ȷ���ǣ�������
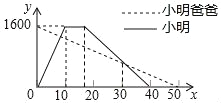
A. ��������1600��
B. С������![]() ���Ӻ���ְֵ�һ������
���Ӻ���ְֵ�һ������
C. С���ڹ�ͣ����ʱ��Ϊ5����
D. С����ְֵڶ�������ʱ����ҵľ�����960��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ���Ź��ŵĽ���ͼ�������Ŷ�����������������״����ˮ��Ŀ���Ϊ10mʱ���Ŷ���ˮ��
����������5m��
��1������������ͬѧ�ǵó����ֽ���ƽ��ֱ������ϵ�ķ���������ͼ��
��ѡ��ķ�����_____�����һ��������������������B��������______���������ѡ�����е������ߵı���ʽ��
��2����Ϊ����ˮ��й����ˮ����ȱ�Ϊ6m����ˮ�����ǵĸ߶���


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�������������ֱ�ΪA��1��1����B��4��2����C��3��4����
��1���뻭����ABC��O����ʱ����ת90��õ���A1B1C1���뻭����A1B1C1��
��2����x��������һ��P��ʹ��PA1C1���ܳ���С����ֱ��д��P�����꣮

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com