练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

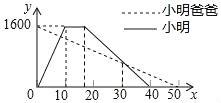
    【题目】小明从家出发到公园晨练，在公园锻炼一段时间后按原路返回，同时小明爸爸从公园按小明的路线返回家中，如图是两人离家的距离y（米）与小明出发的时间x（分）之间的函数图象，则下列结论中不正确的是（　　）

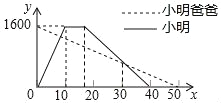
    A. 公园离小明家1600米

    B. 小明出发分钟后与爸爸第一次相遇

    C. 小明在公园停留的时间为5分钟

    D. 小明与爸爸第二次相遇时，离家的距离是960米

    【答案】D

    【解析】

    依据图象可得：公园离小明家1600米；依据小明从家出发到公园晨练时的速度，以及小明爸爸从公园按小明的路线返回家中的速度，即可得到小明出后与爸爸第一次相遇的时间；由图可得：30分钟后小明与爸爸第二次相遇时，离家的距离是640米；依据小明在与爸爸第二次相遇后回到家的时间，以及小明在公园锻炼一段时间后按原路返回的速度，即可得到小明在公园停留的时间为15﹣10=5分钟．

    解：由图可得：公园离小明家1600米，故A选项正确；

    ∵小明从家出发到公园晨练时，速度为1600÷10=160米/分，小明爸爸从公园按小明的路线返回家中的速度为1600÷50=32米/分，

    ∴小明出后与爸爸第一次相遇的时间为1600÷（160+32）=分钟，故B选项正确；

    由图可得：30分钟后小明与爸爸第二次相遇时，离家的距离是1600﹣30×32=640米，故D选项错误；

    ∵小明在与爸爸第二次相遇后回到家的时间为：40﹣30=10分，

    ∴小明在公园锻炼一段时间后按原路返回的速度为640÷10=64米/分，

    ∴40﹣1600÷64=15分，

    ∴小明在公园停留的时间为15﹣10=5分钟，故C选项正确．

    故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

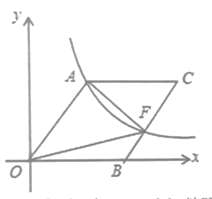
    【题目】如图，在直角坐标系中，四边形OACB为菱形，OB在x轴的正半轴上，∠AOB=60°，过点A的反比例函数y= 的图像与BC交于点F，则△AOF的面积为 ______________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的函数y＝+x，如表是y与x的几组对应值：

    x

    …

    ﹣4

    ﹣3

    -2

    -

    -1

    -

    -

    1

    2

    3

    4

    …

    y

    …

    -

    -

    -

    -

    -2

    -

    -

    2

    …

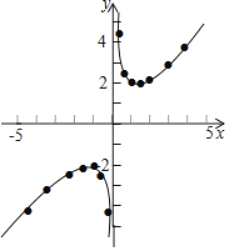
    如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点画出了此函数的图象请你根据学习函数的经验，根据画出的函数图象特征，对该函数的图象与性质进行探究：

    （1）该函数的图象关于 对称；

    （2）在y轴右侧，函数变化规律是当0＜x＜1，y随x的增大而减小；当x＞1，y随x的增大而增大．在y轴左侧，函数变化规律是 ．

    （3）函数y＝当x 时，y有最 值为 ．

    （4）若方程+x＝m有两个不相等的实数根，则m的取值范围是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

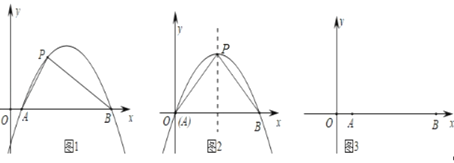
    【题目】如图1，抛物线y＝ax2+bx+c(a≠0)与x轴交于A，B两点，点P在抛物线上(与A，B两点不重合)，若△ABP的三边满足AP2+BP2＝AB2，则我们称点P为抛物线y＝ax2+bx+c(a≠0)的勾股点．

    (1)直接写出抛物线y＝x2﹣1的勾股点坐标为_____；

    (2)如图2，已知抛物线：y＝ax2+bx(a＜0，b＞0)与x轴交于A、B两点，点P为抛物线的顶点，问点P能否为抛物线的勾股点，若能，求出b的值；

    (3)如图3，在平面直角坐标系中，点A(2，0)，B(12，0)，点P到x轴的距离为1，点P是过A、B两点的抛物线上的勾股点，求过P、A、B三点的抛物线的解析式和点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】襄阳市精准扶贫工作已进入攻坚阶段．贫困户张大爷在某单位的帮扶下，把一片坡地改造后种植了优质水果蓝莓，今年正式上市销售．在销售的30天中，第一天卖出20千克，为了扩大销量，采取了降价措施，以后每天比前一天多卖出4千克．第x天的售价为y元/千克，y关于x的函数解析式为 且第12天的售价为32元/千克，第26天的售价为25元/千克．已知种植销售蓝莓的成木是18元/千克，每天的利润是W元（利润=销售收入﹣成本）．

    （1）m=　 　，n=　 　；

    （2）求销售蓝莓第几天时，当天的利润最大？最大利润是多少？

    （3）在销售蓝莓的30天中，当天利润不低于870元的共有多少天？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

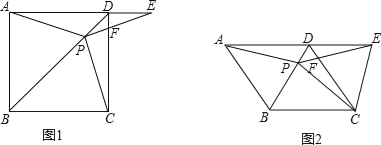
    【题目】如图1，在正方形ABCD中，P是对角线BD上的一点，点E在AD的延长线上，且PA=PE，PE交CD于F．

    （1）证明：PC=PE；

    （2）求∠CPE的度数；

    （3）如图2，把正方形ABCD改为菱形ABCD，其他条件不变，当∠ABC=120°时，连接CE，试探究线段AP与线段CE的数量关系，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

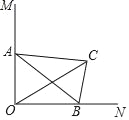
    【题目】如图，在Rt△ABC中，BC＝3，∠BAC＝30°，斜边AB的两个端点分别在相互垂直的射线OM，ON上滑动．下列结论：①若C、O两点关于AB对称，则OA＝3；②若AB平分CO，则AB⊥CO；③C，O两点间的最大距离是6；④斜边AB的中点D运动的路径长是π，其中正确的有（　　）

    A. ①②B. ③④C. ②③④D. ①③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

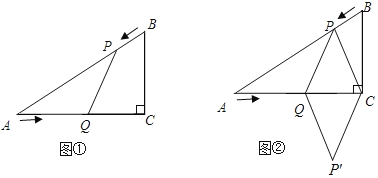
    【题目】已知：如图①，在Rt△ABC中，∠C＝90°，AC＝8cm，BC＝6cm，点P由B出发沿BA方向向点A匀速运动，速度为1cm/s；点Q由A出发沿AC方向向点C匀速运动，速度为2cm/s；连接PQ．若设运动的时间为t（s）（0＜t＜4），解答下列问题：

    （1）当t为何值时，PQ∥BC；

    （2）设△AQP的面积为y（cm2），求y与t之间的函数关系式；

    （3）是否存在某一时刻t，使线段PQ恰好把Rt△ACB的周长和面积同时平分？若存在，求出此时t的值；若不存在，说明理由；

    （4）如图②，连接PC，并把△PQC沿QC翻折，得到四边形PQP′C，那么是否存在某一时刻t，使四边形PQP′C为菱形？若存在，求出此时菱形的边长；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

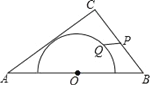
    【题目】如图，在△ABC中，AB=10，AC=8，BC=6，以边AB的中点O为圆心，作半圆与AC相切，点P，Q分别是边BC和半圆上的动点，连接PQ，则PQ长的最小值是_______.

    查看答案和解析>>

    同步练习册答案