
【题目】求证:对角线互相垂直圆内接四边形,自对角线的交点向一边作垂线,其延长线必平分对边.
要求:(1)在给出的圆内接四边形作出PE⊥BC于点E,并延长EP与AD交于点F,不写作法,保留作图痕迹
(2)利用(1)中所作的图形写出已知、求证和证明过程.
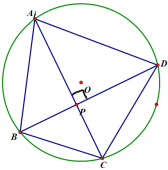
【答案】(1)见解析;(2)DF=FP=AF,点F为AD的中点,过程见解析
【解析】
(1)过P作BC的垂线即可得到答案;(2)根据题意写好已知,求证,利用圆周角定理及直角三角形的性质证明
解:(1)补全的图形如图所示;
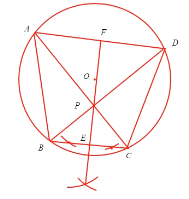
(2)已知:四边形ABCD为圆内接四边形,AC⊥BD,PE⊥BC.延长EP交AD于点F.
求证:点F为AD的中点
证明:∵AC⊥BD,PE⊥BC
∴∠CPD=∠CEF=∠APD=90°
∵EF是线段
∴∠CPE+∠CPD+∠DPF=180°,即∠CPE+∠DPF=90°
∵在Rt△CEP中,∠CPE+∠ECP=90°
∴∠ECP=∠DPF
∵∠ACB与∠ADB为同弧所对的圆周角
∴∠ACB=∠ADB,即∠ECP=∠PDF
∴∠DPF=∠PDF
∴△DPF为等腰三角形,DF=FP
∵∠APF=∠APD -∠DPF=90°-∠DPF,∠PAF=90°-∠PDF
∴∠APF=∠PAF
∴△APF为等腰三角形,PF=AF
即DF=FP=AF,点F为AD的中点.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】华联超市用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该商场购进甲、乙两种商品各多少件?
(2)该超市将购进的甲、乙两种商品全部卖完后一共可获得多少利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了解学生的课外阅读情况,王老师随机抽查部分学生,并对其暑假期间的课外阅读量进行统计分析,绘制成如图所示但不完整的统计图.已知抽查的学生在暑假期间阅读量为2本的人数占抽查总人数的20%,根据所给出信息,解答下列问题:
(1)求被抽查学生人数并直接写出被抽查学生课外阅读量的中位数;
(2)将条形统计图补充完整;
(3)若规定:假期阅读3本及3本以上课外书者为完成假期作业,据此估计该校1500名学生中,完成假期作业的有多少名学生?

查看答案和解析>>
科目:初中数学 来源: 题型:
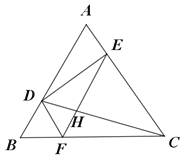
【题目】如图,等边三角形ABC的边长为6,点E为AC边上一点,AE=2,作DE⊥AC于点E交AB于点D,点F在BC边上且BF=BD.连接EF与CD交于点H,则DH的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于新冠状病毒疫情的影响,城际公交车正常行驶时间与行驶道路受到限制.如图,是某企业职工上班时乘车、步行、骑车的人数分布直方图和扇形分布图(两图都不完整),则下列结论中错误的是( )
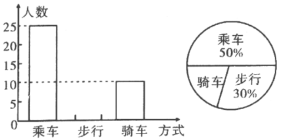
A.该企业总人数为50人B.骑车人数占总人数的20%
C.步行人数为30人D.乘车人数是骑车人数的2.5倍
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,等腰Rt△ABC与等腰Rt△CDE关于原点O成位似关系,相似比为1:3,∠ACB=∠CED=90°,A、C、E是x轴正半轴上的点,B、D是第一象限的点,BC=2,则点D的坐标是( )
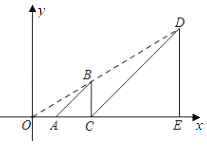
A.(9,6)B.(8,6)C.(6,9)D.(6,8)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.为了解一批口罩的质量适合采用的调查方式是全面调查
B.“任意画一个三角形,其内角和为180°”是随机事件
C.袋中有形状、大小、质地完全一样的6个红球和1个白球,从中随机抽出一个球,一定是红球
D.甲、乙两人进行射击练习,在相同条件下各射击10次,他们成绩的平均数相同,方差分别是![]() ,
,![]() ,则甲的射击成绩较稳定
,则甲的射击成绩较稳定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com