
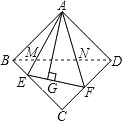
【题目】(1)如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求∠EAF的度数.
(2)如图②,在Rt△ABD中,∠BAD=90°,AB=AD,点M,N是BD边上的任意两点,且∠MAN=45°,将△ABM绕点A逆时针旋转90°至△ADH位置,连接NH,试判断MN,ND,DH之间的数量关系,并说明理由.
(3)在图①中,连接BD分别交AE,AF于点M,N,若EG=4,GF=6,BM=3![]() ,求AG,MN的长.
,求AG,MN的长.

【答案】(1)45°(2)MN2=ND2+DH2(3)![]()
【解析】
试题分析:(1)根据高AG与正方形的边长相等,证明三角形全等,进而证明角相等,从而求出解.
(2)用三角形全等和正方形的对角线平分每一组对角的知识可证明结论.
(3)设出线段的长,结合方程思想,用数形结合得到结果.
试题解析:(1)在Rt△ABE和Rt△AGE中,AB=AG,AE=AE,
∴Rt△ABE≌Rt△AGE(HL).
∴∠BAE=∠GAE.
同理,∠GAF=∠DAF.
∴![]() .
.
(2)MN2=ND2+DH2.
∵∠BAM=∠DAH,∠BAM+∠DAN=45°,
∴∠HAN=∠DAH+∠DAN=45°.
∴∠HAN=∠MAN.
又∵AM=AH,AN=AN,
∴△AMN≌△AHN.
∴MN=HN.
∵∠BAD=90°,AB=AD,
∴∠ABD=∠ADB=45°.
∴∠HDN=∠HDA+∠ADB=90°.
∴NH2=ND2+DH2.
∴MN2=ND2+DH2.
(3)由(1)知,BE=EG,DF=FG.
设AG=x,则CE=x﹣4,CF=x﹣6.
在Rt△CEF中,
∵CE2+CF2=EF2,
∴(x﹣4)2+(x﹣6)2=102.
解这个方程,得x1=12,x2=﹣2(舍去负根).
即AG=12.
在Rt△ABD中,
∴![]() .
.
在(2)中,MN2=ND2+DH2,BM=DH,
∴MN2=ND2+BM2.
设MN=a,则![]() .
.
即a 2=(9![]() ﹣a) 2+(3
﹣a) 2+(3![]() ) 2,
) 2,
∴![]() .即MN=5
.即MN=5![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE= 度;
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则α,β之间有怎样的数量关系?请直接写出你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=13厘米,BC=10厘米,AD⊥BC于点D,动点P从点A出发以每秒1厘米的速度在线段AD上向终点D运动.设动点运动时间为t秒.

(1)求AD的长;
(2)当△PDC的面积为15平方厘米时,求t的值;
(3)动点M从点C出发以每秒2厘米的速度在射线CB上运动.点M与点P同时出发,且当点P运动到终点D时,点M也停止运动.是否存在t,使得![]() ?若存在,请求出t的值;若不存在,请说明理由.
?若存在,请求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校科技小组研制了一套信号发射、接收系统.在对系统进行测试中,如图,小明从路口A处出发,沿东南方向笔直公路行进,并发射信号,小华同时从A处出发,沿西南方向笔直公路行进,并接收信号.若小明步行速度为39米/分,小华步行速度为52米/分,恰好在出发后30分时信号开始不清晰.
(1)你能求出他们研制的信号收发系统的信号传送半径吗?(以信号清晰为界限)
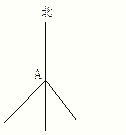
(2)通过计算,你能找到题中数据与勾股数3、4、5的联系吗?试从中寻找求解决问题的简便算法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据4月13日新华社报道,我国由陈薇院士组织的腺病毒载体重组新冠病毒疫苗率先进入第二期临床试验.我们从中选取甲、乙、丙三组各有7名志愿者,测得三组志愿者的体重数据的平均数都是58,方差分别为S甲2=36,S乙2=25,S丙2=16,则数据波动最小的一组是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com