
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 和点
和点![]() 是
是![]() 上的两点,过点
上的两点,过点![]() 作
作![]() 的切线交
的切线交![]() 延长线于点
延长线于点![]() 。
。
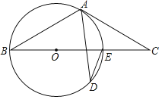
Ⅰ.若![]() ,求
,求![]() 的度数;
的度数;
Ⅱ.若![]() ,求
,求![]() 的度数.
的度数.
【答案】Ⅰ. 40°;Ⅱ. 30°
【解析】
Ⅰ.连接OA,根据圆周角定理求出∠AOC,根据切线的性质求出∠OAC,根据三角形内角和定理求出即可;
Ⅱ.根据![]() ,OA=OB,得出∠B=∠C=∠BAO,再根据三角形的外角可得出∠AOC=2∠C,再根据直角三角形的两个锐角互余,得出∠C=30°,从而得出∠AOC的度数,根据圆周角定理求出
,OA=OB,得出∠B=∠C=∠BAO,再根据三角形的外角可得出∠AOC=2∠C,再根据直角三角形的两个锐角互余,得出∠C=30°,从而得出∠AOC的度数,根据圆周角定理求出![]() 即可
即可
解:(1)连接OA,
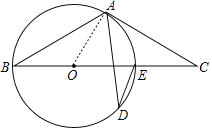
∵∠ADE=25°,
∴由圆周角定理得:∠AOC=2∠ADE=50°,
∵AC切⊙O于A,
∴∠OAC=90°,
∴∠C=180°-∠AOC-∠OAC=180°-50°-90°=40°;
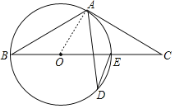
Ⅱ. ∵AB=AC,
∴∠B=∠C,
∵OA=OB,
∴∠BAO=∠B,
∵∠AOC=∠B+∠BAO,
∴∠AOC=2∠B,
∴∠AOC=2∠C,
∵∠OAC=90°,
∴∠AOC+∠C=90°,
∴3∠C=90°,
∴∠C=30°,
∴∠AOC=60°
∴由圆周角定理得:![]() ∠AOC=30°
∠AOC=30°


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若⊙C上存在一个点M,使得MP=MC,则称点P为⊙C的“等径点”,已知点D(![]() ,
,![]() ),E(0,2
),E(0,2![]() ),F(﹣2,0).
),F(﹣2,0).
(1)当⊙O的半径为1时,
①在点D,E,F中,⊙O的“等径点”是哪几个点;
②作直线EF,若直线EF上的点T(m,n)是⊙O的“等径点”,求m的取值范围.
(2)过点E作EG⊥EF交x轴于点G,若△EFG各边上所有的点都是某个圆的“等径点”,求这个圆的半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一辆超市购物车放置在水平地面上,其侧面四边形ABCD与地面某条水平线l在同一平面内,且AB∥l,若∠A=93°,∠D=111°,则直线CD与l所夹锐角的度数为( )

A. 15°B. 18°C. 21°D. 24°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】砸“金蛋”游戏:把210个“金蛋”连续编号为1,2,3,…,210,接着把编号是3的整数倍的“金蛋”全部砸碎;然后将剩下的“金蛋”重新连续编号为1,2,3,…,接着把编号是3的整数倍的“金蛋”全部砸碎……按照这样的方法操作,直到无编号是3的整数倍的“金蛋”为止.操作过程中砸碎编号是“66”的“金蛋”共_____个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,解答问题:
为解方程![]() ,我们可以将
,我们可以将![]() 视为一个整体,然后设
视为一个整体,然后设![]() ,则
,则![]() ,原方程可化为
,原方程可化为![]() ,解此方程得
,解此方程得![]() .当
.当![]() 时,
时,![]() ,∴
,∴![]() ;当
;当![]() 时,
时,![]() ,∴
,∴![]() ,∴原方程的解为
,∴原方程的解为![]() .
.
(1)填空:在原方程得到方程(*)的过程中,利用________法达到了降次的目的,体现了________的数学思想;
(2)解方程:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
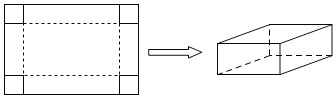
【题目】如图,工人师傅用一块长为10分米,宽为6分米的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形;(厚度不计)
(1)当长方体底面面积为12平方分米时,裁掉的正方形边长为______分米;
(2)若要求制作的长方体的底面长不大于底面宽的5倍,且将容器的外表面进行防锈处理,其侧面处理费用为0.5元/平方分米,底面处理费用为2元/平方分米;求:裁掉的正方形边长为多大时,防锈处理总费用最低,最低为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若要在宽AD为20米的城南大道两边安装路灯,路灯的灯臂BC长2米,且与灯柱AB成120°角,路灯采用圆锥形灯罩,灯罩的轴线CO与灯臂BC垂直,当灯罩的轴线CO通过公路路面的中心线时照明效果最好,此时,路灯的灯柱AB高应该设计为多少米(结果保留根号)?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com