
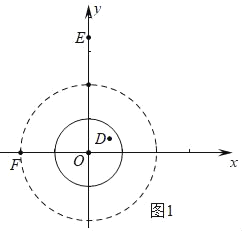
ĄŸÌâÄżĄż¶ÔÓÚÆœĂæÖ±œÇŚű±êÏ”xOyÖДĔăPșÍĄŃCŁŹžűłöÈç϶šÒćŁșÈôĄŃCÉÏŽæÔÚÒ»žö”ăMŁŹÊč”ĂMPŁœMCŁŹÔòłÆ”ăPÎȘĄŃC”ÄĄ°”ÈŸ¶”㥱ŁŹÒŃÖȘ”ăDŁš![]() ŁŹ
ŁŹ![]() Ł©ŁŹEŁš0ŁŹ2
Ł©ŁŹEŁš0ŁŹ2![]() Ł©ŁŹFŁš©2ŁŹ0Ł©Łź
Ł©ŁŹFŁš©2ŁŹ0Ł©Łź
Łš1Ł©”±ĄŃO”İ럶ÎȘ1ʱŁŹ
ąÙÔÚ”ăDŁŹEŁŹFÖĐŁŹĄŃO”ÄĄ°”ÈŸ¶”㥱ÊÇÄÄŒžžö”㣻
ąÚŚśÖ±ÏßEFŁŹÈôÖ±ÏßEFÉϔĔăTŁšmŁŹnŁ©ÊÇĄŃO”ÄĄ°”ÈŸ¶”㥱ŁŹÇóm”ÄÈĄÖ”·¶Î§Łź
Łš2Ł©čę”ăEŚśEGĄÍEFœ»xÖáÓÚ”ăGŁŹÈôĄśEFGžś±ßÉÏËùÓĐ”Ä”ă¶ŒÊÇÄłžöÔȔĥ°”ÈŸ¶”㥱ŁŹÇóŐâžöÔČ”Ä°ëŸ¶r”ÄÈĄÖ”·¶Î§Łź
ĄŸŽđ°žĄżŁš1Ł©ąÙĄŃO”ÄĄ°”ÈŸ¶”㥱ÊÇDŁŹEŁ»ąÚ©2ĄÜmĄÜ©1Ł»Łš2Ł©rĄĘ2Łź
ĄŸœâÎöĄż
Łš1Ł©ąÙžùŸĘĄ°”ÈŸ¶”㥱”ĶšÒćżÉÖȘŁŹĄ°”ÈŸ¶”㥱”œÔČĐĔğàÀëĐĄÓÚ”ÈÓÚÔČ”Ä°ëŸ¶”Ä2±¶ŁŹÓÉŽËŒŽżÉĆжšŁ»
ąÚÈçÍŒ2ÖĐŁŹÉèÖ±ÏßEFœ»°ëŸ¶ÎȘ2”ÄĄŃOÓÚ”ăKŁŹÁŹœÓOKŁŹŚśKMĄÍOFÓÚMŁź”±”ăTÔÚÏ߶ÎFKÉÏʱŁŹ”ăTÊÇĄ°”ÈŸ¶”㥱ŁŹÇółö”ăK”ÄŚű±êŒŽżÉœâŸöÎÊÌ⣻
Łš2Ł©ÒòÎȘĄśEFGžś±ßÉÏËùÓĐ”Ä”ă¶ŒÊÇÄłžöÔȔĥ°”ÈŸ¶”㥱ŁŹËùÒÔŐâžöÔČ”ÄÔČĐÄQÊÇÏ߶ÎFG”ÄÖĐ”ăŁŹÒŚÖȘQŁš2ŁŹ0Ł©ŁŹÉèŐâžöÔČ”Ä°ëŸ¶ÎȘrŁźžùŸĘQGĄÜ2rŁŹččœšČ»”ÈÊœŒŽżÉœâŸöÎÊÌâ.
Łš1Ł©žùŸĘĄ°”ÈŸ¶”㥱”ĶšÒćżÉÖȘŁŹĄ°”ÈŸ¶”㥱”œÔČĐĔğàÀëĐĄÓÚ”ÈÓÚÔČ”Ä°ëŸ¶”Ä2±¶ŁźŒŽ°ëŸ¶ÎȘ1”ÄĄŃO”ÄĄ°”ÈŸ¶”㥱ÔÚÒÔOÎȘÔČĐÄ2ÎȘ°ëŸ¶”ÄÔČÄÚ»òÔČÉÏŁź
ÈçÍŒ1ÖĐŁŹčÛČìÍŒÏóżÉÖȘŁșÔÚ”ăDŁŹEŁŹFÖĐŁŹĄŃO”ÄĄ°”ÈŸ¶”㥱ÊÇDŁŹEŁź
ąÚÈçÍŒ2ÖĐŁŹÉèÖ±ÏßEFœ»°ëŸ¶ÎȘ2”ÄĄŃOÓÚ”ăKŁŹÁŹœÓOKŁŹŚśKMĄÍOFÓÚMŁź
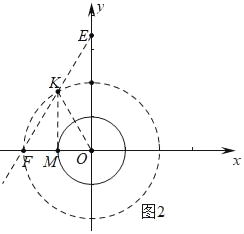
ĄßOFŁœ2ŁŹOEŁœ2![]() ŁŹ
ŁŹ
ĄàtanĄÏEFOŁœ![]() =
=![]() ŁŹ
ŁŹ
ĄàĄÏOFKŁœ60ĄăŁŹ
ĄßOFŁœOKŁŹ
ĄàĄśOFKÊǔȱßÈęœÇĐÎŁŹ
ĄàOFŁœOKŁœFKŁœ2ŁŹ
ĄßKMĄÍOFŁŹ
ĄàFMŁœOMŁœ1ŁŹKMŁœ![]() Łœ
Łœ![]() ŁŹ
ŁŹ
ĄàKŁš©1ŁŹ![]() Ł©ŁŹ
Ł©ŁŹ
Ąß”±”ăTÔÚÏ߶ÎFKÉÏʱŁŹ”ăTÊÇĄ°”ÈŸ¶”㥱ŁŹ
Ąà©2ĄÜmĄÜ©1Łź
Łš2Ł©ÈçÍŒ3ÖĐŁŹ
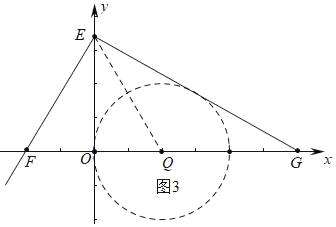
ĄßĄśEFGÊÇÖ±œÇÈęœÇĐÎŁŹĄÏFEGŁœ90ĄăŁŹĄÏEFGŁœ60ĄăŁŹ
ĄàEFŁœ2OFŁœ4ŁŹFGŁœ2EFŁœ8ŁŹ
ĄàOGŁœ6ŁŹ
ÓÉÌâÒ⥜EFGžś±ßÉÏËùÓĐ”Ä”ă¶ŒÊÇÄłžöÔȔĥ°”ÈŸ¶”㥱ŁŹŐâžöÔČ”ÄÔČĐÄQÊÇÏ߶ÎFG”ÄÖД㣏QŁš2ŁŹ0Ł©ŁŹÉèŐâžöÔČ”Ä°ëŸ¶ÎȘrŁź
ÓÉÌâÒâŁșQGĄÜ2r
Ąà4ĄÜ2rŁŹ
ĄàrĄĘ2ŁŹ
ŒŽŐâžöÔČ”Ä°ëŸ¶r”ÄÈĄÖ”·¶Î§ÎȘrĄĘ2Łź



| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÎÊÌⱳŸ°
ÈçÍŒŁš1Ł©ŁŹÔÚËıßĐÎABCDÖĐŁŹĄÏB+ĄÏDŁœ180ĄăŁŹABŁœADŁŹĄÏBADŁœŠÁŁŹÒÔ”ăAÎȘ¶„”ăŚśÒ»žöœÇŁŹœÇ”ÄÁœ±ß·Ö±đœ»BCŁŹCDÓÚ”ăEŁŹFŁŹÇÒĄÏEAF![]() ŠÁŁŹÁŹœÓEFŁŹÊÔÌœŸżŁșÏ߶ÎBEŁŹDFŁŹEFÖźŒä”ÄÊęÁżčŰÏ”Łź
ŠÁŁŹÁŹœÓEFŁŹÊÔÌœŸżŁșÏ߶ÎBEŁŹDFŁŹEFÖźŒä”ÄÊęÁżčŰÏ”Łź

Łš1Ł©ÌŰÊâÇ韰
ÔÚÉÏÊöÌőŒțÏÂŁŹĐĄĂśÔöŒÓÌőŒțĄ°”±ĄÏBADŁœĄÏBŁœĄÏDŁœ90ĄăʱĄ±ÈçÍŒŁš2Ł©ŁŹĐĄĂśșÜżìĐŽłöÁËŁșBEŁŹDFŁŹEFÖźŒä”ÄÊęÁżčŰÏ”ÎȘ______Łź
Łš2Ł©Àà±ÈČÂÏë
Àà±ÈÌŰÊâÇ韰ŁŹĐĄĂśČÂÏëŁșÔÚÈçÍŒŁš1Ł©”ÄÌőŒțÏÂÏ߶ÎBEŁŹDFŁŹEFÖźŒä”ÄÊęÁżčŰÏ”ÊÇ·ńÈÔÈ»łÉÁąŁżÈôłÉÁąŁŹÇëÄă°ïÖúĐĄĂśÍêłÉրÜŁ»ÈôČ»łÉÁąŁŹÇë˔ÜÀíÓÉŁź
Łš3Ł©œâŸöÎÊÌâ
ÈçÍŒŁš3Ł©ŁŹÔÚĄśABCÖĐŁŹĄÏBACŁœ90ĄăŁŹABŁœACŁœ4ŁŹ”ăDŁŹEŸùÔÚ±ßBCÉÏŁŹÇÒĄÏDAEŁœ45ĄăŁŹÈôBD![]() ŁŹÇëÖ±œÓĐŽłöDE”Äł€Łź
ŁŹÇëÖ±œÓĐŽłöDE”Äł€Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹœûÖčȶÓăÆÚŒäŁŹÄłșŁÉÏ»üČé¶ÓÔÚÄłșŁÓòŃČÂߣŹÉÏÎçÄłÒ»Ê±żÌÔÚAŽŠœÓ”œÖž»Óȿ͚ÖȘŁŹÔÚËûĂǶ«±±·œÏòŸàÀë12șŁÀï”ÄBŽŠÓĐÒ»ËÒȶÓ㎏ŁŹŐęÔÚŃŰÄÏÆ«¶«75Ąă·œÏòÒÔĂżĐĄÊ±10șŁÀï”ÄËÙ¶ÈșœĐĐŁŹ»üČé¶ÓÔ±ÁąŒŽłËŚűŃČÂߎŹÒÔĂżĐĄÊ±14șŁÀï”ÄËÙ¶ÈŃ۱±Æ«¶«ÄłÒ»·œÏòłö·ąŁŹÔÚCŽŠłÉčŠÀčœŰȶÓ㎏ŁŹÔòŃČÂߎŹŽÓłö·ą”œłÉčŠÀčœŰȶÓ㎏ËùÓĂ”ÄʱŒäÊÇŁšĄĄĄĄŁ©

A. 1ĐĄÊ± B. 2ĐĄÊ± C. 3ĐĄÊ± D. 4ĐĄÊ±
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
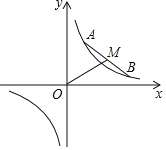
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚÆœĂæÖ±œÇŚű±êÏ”ÖĐŁŹ”ă![]() ŁŹ
ŁŹ![]() ÔÚ·Ž±ÈÀęșŻÊę
ÔÚ·Ž±ÈÀęșŻÊę![]() ”ÄÍŒÏóÉÏÔ˶ŻŁŹÇÒÊŒÖŐ±ŁłÖÏ߶Î
”ÄÍŒÏóÉÏÔ˶ŻŁŹÇÒÊŒÖŐ±ŁłÖÏ߶Î![]() ”Äł€¶ÈČ»±äŁź
”Äł€¶ÈČ»±äŁź![]() ÎȘÏ߶Î
ÎȘÏ߶Î![]() ”ÄÖД㣏ÁŹœÓ
”ÄÖД㣏ÁŹœÓ![]() ŁźÔòÏ߶Î
ŁźÔòÏ߶Î![]() ł€¶È”ÄŚîĐĄÖ”ÊÇ_____(ÓĂșŹ
ł€¶È”ÄŚîĐĄÖ”ÊÇ_____(ÓĂșŹ![]() ”ÄŽúÊęÊœ±íÊŸ)Łź
”ÄŽúÊęÊœ±íÊŸ)Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚÆœĂæÖ±œÇŚű±êÏ”xOyÖĐŁŹ”ăBŁšŁ1ŁŹ4Ł©ŁŹ”ăAŁšŁ7ŁŹ0Ł©ŁŹ”ăPÊÇÖ±Ïß![]() ÉÏÒ»”㣏ÇÒĄÏABPŁœ45ĄăŁŹÔò”ăP”ÄŚű±êÎȘ____.
ÉÏÒ»”㣏ÇÒĄÏABPŁœ45ĄăŁŹÔò”ăP”ÄŚű±êÎȘ____.

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒŃÖȘĆŚÎïÏß![]() ”ĶԳÆÖáÎȘ
”ĶԳÆÖáÎȘ![]() ŁŹÓë
ŁŹÓë![]() Öá”ÄÒ»žöœ»”ăÔÚ
Öá”ÄÒ»žöœ»”ăÔÚ![]() șÍ
șÍ![]() ÖźŒäŁŹÆäČż·ÖÍŒÏńÈçÍŒËùÊŸŁŹÔòÏÂÁĐœáÂÛŁșąÙ”ă
ÖźŒäŁŹÆäČż·ÖÍŒÏńÈçÍŒËùÊŸŁŹÔòÏÂÁĐœáÂÛŁșąÙ”ă![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ÊÇžĂĆŚÎïÏßÉÏ”Ä”ăŁŹÔò
ÊÇžĂĆŚÎïÏßÉÏ”Ä”ăŁŹÔò![]() Ł»ąÚ
Ł»ąÚ![]() Ł»ąÛ
Ł»ąÛ![]() Łš
Łš![]() ÎȘÈÎÒâÊ”Ê꣩.ÆäÖĐŐęÈ·œáÂ۔ĞöÊęÊÇŁš Ł©
ÎȘÈÎÒâÊ”Ê꣩.ÆäÖĐŐęÈ·œáÂ۔ĞöÊęÊÇŁš Ł©
A. 0B. 1C. 2D. 3
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒŃÖȘ¶țŽÎșŻÊę![]() ”ÄŚîŽóÖ”ÎȘ4ŁŹÇÒžĂĆŚÎïÏßÓë
”ÄŚîŽóÖ”ÎȘ4ŁŹÇÒžĂĆŚÎïÏßÓë![]() Öá”Äœ»”ăÎȘ
Öá”Äœ»”ăÎȘ![]() ŁŹ¶„”ăÎȘ
ŁŹ¶„”ăÎȘ![]() .
.
Łš1Ł©ÇóžĂ¶țŽÎșŻÊę”ÄœâÎöÊœŒ°”ă![]() ŁŹ
ŁŹ![]() ”ÄŚű±êŁ»
”ÄŚű±êŁ»
Łš2Ł©”ă![]() ÊÇ
ÊÇ![]() ÖáÉϔĶŻ”㣏
ÖáÉϔĶŻ”㣏
ąÙÇó![]() ”ÄŚîŽóÖ”Œ°¶ÔÓŠ”Ä”ă
”ÄŚîŽóÖ”Œ°¶ÔÓŠ”Ä”ă![]() ”ÄŚű±êŁ»
”ÄŚű±êŁ»
ąÚÉè![]() ÊÇ
ÊÇ![]() ÖáÉϔĶŻ”㣏ÈôÏ߶Î
ÖáÉϔĶŻ”㣏ÈôÏ߶Î![]() ÓëșŻÊę
ÓëșŻÊę![]() ”ÄÍŒÏńÖ»ÓĐÒ»žöč«čȔ㣏Çó
”ÄÍŒÏńÖ»ÓĐÒ»žöč«čȔ㣏Çó![]() ”ÄÈĄÖ”·¶Î§.
”ÄÈĄÖ”·¶Î§.
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
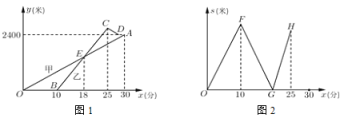
ĄŸÌâÄżĄżÄłĐŁ”ÄŒŚĄąÒÒÁœÎ»ÀÏÊŠÍŹŚĄÒ»ĐĄÇűŁŹžĂĐĄÇűÓëѧУÏàŸà2400ĂŚ. ŒŚŽÓĐĄÇűČœĐĐÈ„Ń§ĐŁŁŹłö·ą10·ÖÖÓșóÒÒÔÙłö·ąŁŹÒÒŽÓĐĄÇűÏÈÆïč«čČŚÔĐĐł”ŁŹÍŸŸŃ§ĐŁÒćÆïĐĐÈôžÉĂŚ”œŽï»čł””ășóŁŹÁąŒŽČœĐĐŚß»ŰѧУ. ÒŃÖȘŒŚČœĐĐ”ÄËٶȱÈÒÒČœĐĐ”ÄËÙ¶ÈĂż·ÖÖÓżì5ĂŚ. ÉèŒŚČœĐĐ”ÄʱŒäÎȘ![]() (·Ö)ŁŹÍŒ1ÖĐÏ߶Î
(·Ö)ŁŹÍŒ1ÖĐÏ߶Î![]() șÍŐÛÏß
șÍŐÛÏß![]() ·Ö±đ±íÊŸŒŚĄąÒÒÀëżȘĐĄÇű”Ä·łÌ
·Ö±đ±íÊŸŒŚĄąÒÒÀëżȘĐĄÇű”Ä·łÌ![]() (ĂŚ)ÓëŒŚČœĐĐʱŒä
(ĂŚ)ÓëŒŚČœĐĐʱŒä![]() (·Ö)”ÄșŻÊęčŰÏ””ÄÍŒÏóŁ»ÍŒ2±íÊŸŒŚĄąÒÒÁœÈËÖźŒä”ÄŸàÀë
(·Ö)”ÄșŻÊęčŰÏ””ÄÍŒÏóŁ»ÍŒ2±íÊŸŒŚĄąÒÒÁœÈËÖźŒä”ÄŸàÀë![]() (ĂŚ)ÓëŒŚČœĐĐʱŒä
(ĂŚ)ÓëŒŚČœĐĐʱŒä![]() (·Ö)”ÄșŻÊęčŰÏ””ÄÍŒÏó(Č»ÍêŐû).žùŸĘÍŒ1șÍÍŒ2ÖĐËùžűĐĆÏąŁŹœâŽđÏÂÁĐÎÊÌâŁș
(·Ö)”ÄșŻÊęčŰÏ””ÄÍŒÏó(Č»ÍêŐû).žùŸĘÍŒ1șÍÍŒ2ÖĐËùžűĐĆÏąŁŹœâŽđÏÂÁĐÎÊÌâŁș
(1)ÇóŒŚČœĐĐ”ÄËÙ¶ÈșÍÒÒłö·ąÊ±ŒŚÀëżȘĐĄÇű”Ä·łÌŁ»
(2)ÇóÒÒÆïŚÔĐĐł””ÄËÙ¶ÈșÍÒÒ”œŽï»čł””ăʱŒŚĄąÒÒÁœÈËÖźŒä”ÄŸàÀ룻
(3)ÔÚÍŒ2ÖĐŁŹ»łö”±![]() ʱ
ʱ![]() čŰÓÚ
čŰÓÚ![]() ”ÄșŻÊę”ÄŽóÖÂÍŒÏó. (ÎÂÜ°ÌáÊŸŁșÇë»ÔÚŽđÌâŸíÏà¶ÔÓŠ”ÄÍŒÉÏ)
”ÄșŻÊę”ÄŽóÖÂÍŒÏó. (ÎÂÜ°ÌáÊŸŁșÇë»ÔÚŽđÌâŸíÏà¶ÔÓŠ”ÄÍŒÉÏ)
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹ![]() ÊÇ
ÊÇ![]() ”ÄÖ±Ÿ¶ŁŹ”ă
”ÄÖ±Ÿ¶ŁŹ”ă![]() șÍ”ă
șÍ”ă![]() ÊÇ
ÊÇ![]() ÉÏ”ÄÁœ”㣏čę”ă
ÉÏ”ÄÁœ”㣏čę”ă![]() Śś
Śś![]() ”ÄÇĐÏßœ»
”ÄÇĐÏßœ»![]() ŃÓł€ÏßÓÚ”ă
ŃÓł€ÏßÓÚ”ă![]() ĄŁ
ĄŁ
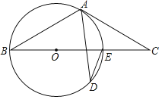
ąń.Èô![]() ŁŹÇó
ŁŹÇó![]() ”ĶÈÊꣻ
”ĶÈÊꣻ
ąò.Èô![]() ŁŹÇó
ŁŹÇó![]() ”ĶÈÊę.
”ĶÈÊę.
Č鿎Žđ°žșÍœâÎö>>
čúŒÊѧУÓĆŃĄ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com