
ЁОЬтФПЁПЮЪЬтБГОА
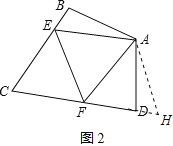
ШчЭМЃЈ1ЃЉЃЌдкЫФБпаЮABCDжаЃЌЁЯB+ЁЯDЃН180ЁуЃЌABЃНADЃЌЁЯBADЃНІСЃЌвдЕуAЮЊЖЅЕузївЛИіНЧЃЌНЧЕФСНБпЗжБ№НЛBCЃЌCDгкЕуEЃЌFЃЌЧвЁЯEAF![]() ІСЃЌСЌНгEFЃЌЪдЬНОПЃКЯпЖЮBEЃЌDFЃЌEFжЎМфЕФЪ§СПЙиЯЕЃЎ
ІСЃЌСЌНгEFЃЌЪдЬНОПЃКЯпЖЮBEЃЌDFЃЌEFжЎМфЕФЪ§СПЙиЯЕЃЎ

ЃЈ1ЃЉЬиЪтЧщОА
дкЩЯЪіЬѕМўЯТЃЌаЁУїдіМгЬѕМўЁАЕБЁЯBADЃНЁЯBЃНЁЯDЃН90ЁуЪБЁБШчЭМЃЈ2ЃЉЃЌаЁУїКмПьаДГіСЫЃКBEЃЌDFЃЌEFжЎМфЕФЪ§СПЙиЯЕЮЊ______ЃЎ
ЃЈ2ЃЉРрБШВТЯы
РрБШЬиЪтЧщОАЃЌаЁУїВТЯыЃКдкШчЭМЃЈ1ЃЉЕФЬѕМўЯТЯпЖЮBEЃЌDFЃЌEFжЎМфЕФЪ§СПЙиЯЕЪЧЗёШдШЛГЩСЂЃПШєГЩСЂЃЌЧыФуАяжњаЁУїЭъГЩжЄУїЃЛШєВЛГЩСЂЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉНтОіЮЪЬт
ШчЭМЃЈ3ЃЉЃЌдкЁїABCжаЃЌЁЯBACЃН90ЁуЃЌABЃНACЃН4ЃЌЕуDЃЌEОљдкБпBCЩЯЃЌЧвЁЯDAEЃН45ЁуЃЌШєBD![]() ЃЌЧыжБНгаДГіDEЕФГЄЃЎ
ЃЌЧыжБНгаДГіDEЕФГЄЃЎ
ЁОД№АИЁПЃЈ1ЃЉBE+DFЃНEFЃЛЃЈ2ЃЉГЩСЂЃЛЃЈ3ЃЉDE![]()
ЁОНтЮіЁП
ЃЈ1ЃЉНЋЁїABEШЦЕуAФцЪБеыа§зЊ90ЁуЃЌЕУЕНЁїADGЃЌгЩа§зЊЕФаджЪПЩЕУAEЃНAGЃЌBEЃНDGЃЌЁЯBAEЃНЁЯDAGЃЌИљОнЁЯEAF=![]() ЁЯBADПЩЕУЁЯBAE+ЁЯDAFЃН45ЁуЃЌМДПЩЕУГіЁЯЁЯEAFЃНЁЯFAGЃЌРћгУSASПЩжЄУїЁїAFEЁеЁїAFGЃЌПЩЕУEF=FGЃЌНјЖјПЩЕУEF=BE+FDЃЛЃЈ2ЃЉНЋЁїABEШЦЕуAФцЪБеыа§зЊІСЕУЕНЁїADHЃЌгЩа§зЊЕФаджЪПЩЕУЁЯABEЃНЁЯADHЃЌЁЯBAEЃНЁЯDAHЃЌAEЃНAHЃЌBEЃНDHЃЌИљОнЁЯBADЃНІСЃЌЁЯEAF
ЁЯBADПЩЕУЁЯBAE+ЁЯDAFЃН45ЁуЃЌМДПЩЕУГіЁЯЁЯEAFЃНЁЯFAGЃЌРћгУSASПЩжЄУїЁїAFEЁеЁїAFGЃЌПЩЕУEF=FGЃЌНјЖјПЩЕУEF=BE+FDЃЛЃЈ2ЃЉНЋЁїABEШЦЕуAФцЪБеыа§зЊІСЕУЕНЁїADHЃЌгЩа§зЊЕФаджЪПЩЕУЁЯABEЃНЁЯADHЃЌЁЯBAEЃНЁЯDAHЃЌAEЃНAHЃЌBEЃНDHЃЌИљОнЁЯBADЃНІСЃЌЁЯEAF![]() ІСПЩЕУЁЯBAE+ЁЯFAD
ІСПЩЕУЁЯBAE+ЁЯFAD![]() ІСЃЌНјЖјПЩжЄУїЁЯFAHЃНЁЯEAFЃЌРћгУSASПЩжЄУїЁїAEFЁеЁїAHFЃЌПЩЕУEF=FH=BE+FDЃЛЃЈ3ЃЉНЋЁїAECШЦЕуAЫГЪБеыа§зЊ90ЁуЃЌЕУЕНЁїAEЁфBЃЌСЌНгDEЁфЃЌгЩа§зЊЕФаджЪПЩЕУBEЁфЃНECЃЌAEЁфЃНAEЃЌЁЯCЃНЁЯABEЁфЃЌЁЯEACЃНЁЯEЁфABЃЌИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪПЩЕУЁЯABCЃНЁЯACBЃН45ЁуЃЌBCЃН4
ІСЃЌНјЖјПЩжЄУїЁЯFAHЃНЁЯEAFЃЌРћгУSASПЩжЄУїЁїAEFЁеЁїAHFЃЌПЩЕУEF=FH=BE+FDЃЛЃЈ3ЃЉНЋЁїAECШЦЕуAЫГЪБеыа§зЊ90ЁуЃЌЕУЕНЁїAEЁфBЃЌСЌНгDEЁфЃЌгЩа§зЊЕФаджЪПЩЕУBEЁфЃНECЃЌAEЁфЃНAEЃЌЁЯCЃНЁЯABEЁфЃЌЁЯEACЃНЁЯEЁфABЃЌИљОнЕШбќжБНЧШ§НЧаЮЕФаджЪПЩЕУЁЯABCЃНЁЯACBЃН45ЁуЃЌBCЃН4![]() ЃЌМДПЩЧѓГіЁЯEЁфBDЃН90ЁуЃЌРћгУSASПЩжЄУїЁїAEFЁеЁїAHFЃЌПЩЕУDEЃНDEЁфЃЌРћгУЙДЙЩЖЈРэЧѓГіDEЕФГЄМДПЩЕФД№АИ.
ЃЌМДПЩЧѓГіЁЯEЁфBDЃН90ЁуЃЌРћгУSASПЩжЄУїЁїAEFЁеЁїAHFЃЌПЩЕУDEЃНDEЁфЃЌРћгУЙДЙЩЖЈРэЧѓГіDEЕФГЄМДПЩЕФД№АИ.
ЃЈ1ЃЉBE+DFЃНEFЃЌ
ШчЭМ1ЃЌНЋЁїABEШЦЕуAФцЪБеыа§зЊ90ЁуЃЌЕУЕНЁїADGЃЌ
ЁпЁЯADCЃНЁЯBЃНЁЯADGЃН90ЁуЃЌ
ЁрЁЯFDGЃН180ЁуЃЌМДЕуFЃЌDЃЌGЙВЯпЃЎ
гЩа§зЊПЩЕУAEЃНAGЃЌBEЃНDGЃЌЁЯBAEЃНЁЯDAGЃЎ
ЁпЁЯBAE+ЁЯDAFЃНЁЯBADЉЁЯEAFЃН90ЁуЉ![]() ЁЯBAD=90Ёу-45ЁуЃН45ЁуЃЌ
ЁЯBAD=90Ёу-45ЁуЃН45ЁуЃЌ
ЁрЁЯDAG+ЁЯDAFЃН45ЁуЃЌМДЁЯFAG=45ЁуЃЌ
ЁрЁЯEAFЃНЁЯFAGЃЌ
ЁрЁїAFEЁеЁїAFGЃЈSASЃЉЃЌ
ЁрEFЃНFGЃЎ
гжЁпFGЃНDG+DFЃНBE+DFЃЌ
ЁрBE+DFЃНEFЃЌ

ЙЪД№АИЮЊЃКBE+DFЃНEFЃЎ
ЃЈ2ЃЉГЩСЂЃЎ
ШчЭМ2ЃЌНЋЁїABEШЦЕуAФцЪБеыа§зЊІСЕУЕНЁїADHЃЌ
ПЩЕУЁЯABEЃНЁЯADHЃЌЁЯBAEЃНЁЯDAHЃЌAEЃНAHЃЌBEЃНDHЃЎ
ЁпЁЯB+ЁЯADCЃН180ЁуЃЌ
ЁрЁЯADH+ЁЯADCЃН180ЁуЃЌ
ЁрЕуCЃЌDЃЌHдкЭЌвЛжБЯпЩЯЃЎ
ЁпЁЯBADЃНІСЃЌЁЯEAF![]() ІСЃЌ
ІСЃЌ
ЁрЁЯBAE+ЁЯFAD![]() ІСЃЌ
ІСЃЌ
ЁрЁЯDAH+ЁЯFAD![]() ІСЃЌ
ІСЃЌ
ЁрЁЯFAHЃНЁЯEAFЃЌ
гжЁпAFЃНAFЃЌ
ЁрЁїAEFЁеЁїAHFЃЈSASЃЉЃЌ
ЁрEFЃНFHЃНDF+DHЃНDF+BEЃЛ
ЃЈ3ЃЉDE![]() ЃЌ
ЃЌ
ШчЭМ3ЃЌНЋЁїAECШЦЕуAЫГЪБеыа§зЊ90ЁуЃЌЕУЕНЁїAEЁфBЃЌСЌНгDEЁфЃЎ
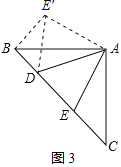
ПЩЕУBEЁфЃНECЃЌAEЁфЃНAEЃЌЁЯCЃНЁЯABEЁфЃЌЁЯEACЃНЁЯEЁфABЃЌ
дкRtЁїABCжаЃЌЁпABЃНACЃН4ЃЌЁЯBAC=90ЁуЃЌ
ЁрЁЯABCЃНЁЯACBЃН45ЁуЃЌBCЃН4![]() ЃЌ
ЃЌ
ЁрCD=BC=BD=3![]() ЃЌ
ЃЌ
ЁрЁЯABC+ЁЯABEЁфЃН90ЁуЃЌМДЁЯEЁфBDЃН90ЁуЃЌ
ЁрEЁфB2+BD2ЃНEЁфD2ЃЎ
взжЄЁїAEЁфDЁеЁїAEDЃЌ
ЁрDEЃНDEЁфЃЌ
ЁрDE2ЃНBD2+EC2ЃЌМДDE2![]() ЃЌ
ЃЌ
НтЕУ![]() ЃЎ
ЃЎ


 бЇЦкИДЯАвЛБОЭЈбЇЯАзмЖЏдБЦкФЉМгЪюМйбгБпШЫУёГіАцЩчЯЕСаД№АИ
бЇЦкИДЯАвЛБОЭЈбЇЯАзмЖЏдБЦкФЉМгЪюМйбгБпШЫУёГіАцЩчЯЕСаД№АИ УЂЙћНЬИЈЪюМйЬьЕижиЧьГіАцЩчЯЕСаД№АИ
УЂЙћНЬИЈЪюМйЬьЕижиЧьГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
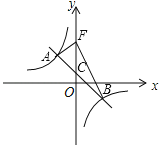
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§yЃНЉx+bЕФЭМЯѓгыЗДБШР§КЏЪ§yЃН![]() (kЁй0)ЕФЭМЯѓНЛгкAЁЂBЕуЃЌгыyжсНЛгкЕуCЃЌЦфжаЕуAЕФАыБъЮЊ(Љ2ЃЌ3)
(kЁй0)ЕФЭМЯѓНЛгкAЁЂBЕуЃЌгыyжсНЛгкЕуCЃЌЦфжаЕуAЕФАыБъЮЊ(Љ2ЃЌ3)
(1)ЧѓвЛДЮКЏЪ§КЭЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
(2)ШчЭМЃЌШєНЋЕуCбиyжсЯђЩЯЦНвЦ4ИіЕЅЮЛГЄЖШжСЕуFЃЌСЌНгAFЁЂBFЃЌЧѓЁїABFЕФУцЛ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§yЃНx2Љ2xЉ3ЃЌШєЯпЖЮABдкxжсЩЯЃЌЧвABЮЊ2![]() ИіЕЅЮЛГЄЖШЃЌвдABЮЊБпзїЕШБпЁїABCЃЌЪЙЕуCТфдкИУКЏЪ§yжсгвВрЕФЭМЯѓЩЯЃЌдђЕуCЕФзјБъЮЊЃЈЁЁЁЁЃЉ
ИіЕЅЮЛГЄЖШЃЌвдABЮЊБпзїЕШБпЁїABCЃЌЪЙЕуCТфдкИУКЏЪ§yжсгвВрЕФЭМЯѓЩЯЃЌдђЕуCЕФзјБъЮЊЃЈЁЁЁЁЃЉ
A. ЃЈ1+![]() ЃЌ3ЃЉЛђЃЈ2ЃЌЉ3ЃЉB. ЃЈ1Љ
ЃЌ3ЃЉЛђЃЈ2ЃЌЉ3ЃЉB. ЃЈ1Љ![]() ЃЌ3ЃЉЛђЃЈ2ЃЌ3ЃЉ
ЃЌ3ЃЉЛђЃЈ2ЃЌ3ЃЉ
C. ЃЈЉ1+![]() ЃЌЉ3ЃЉЛђЃЈ2ЃЌЉ3ЃЉD. ЃЈ1+
ЃЌЉ3ЃЉЛђЃЈ2ЃЌЉ3ЃЉD. ЃЈ1+![]() ЃЌЉ3ЃЉЛђЃЈ2ЃЌ3ЃЉ
ЃЌЉ3ЃЉЛђЃЈ2ЃЌ3ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП ЮЊЫГРћЭЈЙ§ЁАЙњМвЮФУїГЧЪаЁБбщЪеЃЌЪаеўИЎФтЖдГЧЧјВПЗжТЗЖЮЕФШЫааЕРЕизЉЁЂТЬЛЏДјЁЂХХЫЎЙмЕШЙЋгУЩшЪЉШЋУцИќаТИФдьЃЌЯжгаМзЁЂввСНИіЙЄГЬЖггавтГаАќетЯюЙЄГЬЃЌОЕїВщжЊЕРЃЌввЙЄГЬЖгЕЅЖРЭъГЩДЫЯюЙЄГЬЕФЪБМфЪЧМзЙЄГЬЖгЕЅЖРЭъГЩДЫЯюЙЄГЬЪБМфЕФ2БЖЃЌШєМзЁЂввСНЙЄГЬЖгКЯзїжЛаш10ЬьЭъГЩЃЎМзЁЂввСНИіЙЄГЬЖгЕЅЖРЭъГЩДЫЯюЙЄГЬИїашЖрЩйЬьЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃОХФъМЖзщжЏгаНБжЊЪЖОКШќЃЌХЩаЁУїШЅЙКТђAЁЂBСНжжЦЗХЦЕФИжБЪзїЮЊНБЦЗЃЎвбжЊвЛжЇAЦЗХЦИжБЪЕФМлИёБШвЛжЇBЦЗХЦИжБЪЕФМлИёЖр5дЊЃЌЧвТђ100дЊAЦЗХЦИжБЪгыТђ50дЊBЦЗХЦИжБЪЪ§ФПЯрЭЌЃЎ
ЃЈ1ЃЉЧѓAЁЂBСНжжЦЗХЦИжБЪЕФЕЅМлЗжБ№ЮЊЖрЩйдЊЃП
ЃЈ2ЃЉИљОнЛюЖЏЕФЩшНБЧщПіЃЌОіЖЈЙКТђAЁЂBСНжжЦЗХЦЕФИжБЪЙВ100жЇЃЌШчЙћЩшЙКТђAЦЗХЦИжБЪЕФЪ§СПЮЊnжЇЃЌЙКТђетСНжжЦЗХЦЕФИжБЪЙВЛЈЗбyдЊЃЎ
ЂйжБНгаДГіyЃЈдЊЃЉЙигкnЃЈжЇЃЉЕФКЏЪ§ЙиЯЕЪНЃЛ
ЂкШчЙћЫљЙКТђAЦЗХЦИжБЪЕФЪ§СПВЛЩйгкBЦЗХЦИжБЪЪ§СПЕФ![]() ЃЌЧыФуАяжњаЁУїМЦЫуШчКЮЙКТђЃЌВХФмЪЙЫљЛЈЗбЕФЧЎзюЩйЃПДЫЪБЛЈЗбЪЧЖрЩйЃП
ЃЌЧыФуАяжњаЁУїМЦЫуШчКЮЙКТђЃЌВХФмЪЙЫљЛЈЗбЕФЧЎзюЩйЃПДЫЪБЛЈЗбЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШЋУцСНКЂеўВпЪЕЪЉКѓЃЌМзЃЌввСНИіМвЭЅгаСЫИїздЕФЙцЛЎ.МйЖЈЩњФаЩњХЎЕФИХТЪЯрЭЌЃЌЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉМзМвЭЅвбгавЛИіФаКЂЃЌзМБИдйЩњвЛИіКЂзгЃЌдђЕкЖўИіКЂзгЪЧХЎКЂЕФИХТЪЪЧ ЃЛ
ЃЈ2ЃЉввМвЭЅУЛгаКЂзгЃЌзМБИЩњСНИіКЂзгЃЌЧѓжСЩйгавЛИіКЂзгЪЧХЎКЂЕФИХТЪ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаТХЉДхРждАЩшжУСЫвЛИіЧяЧЇГЁЫљЃЌШчЭМЫљЪОЃЌЧяЧЇРЩўOBЕФГЄЮЊ3mЃЌОВжЙЪБЃЌЬЄАхЕНЕиУцОрРыBDЕФГЄЮЊ0.6mЃЈЬЄАхКёЖШКіТдВЛМЦЃЉЃЎЮЊАВШЋЦ№МћЃЌРждАЙмРэДІЙцЖЈЃКЖљЭЏЕФЁААВШЋИпЖШЁБЮЊhmЃЌГЩШЫЕФЁААВШЋИпЖШЁБЮЊ2mЃЈМЦЫуНсЙћОЋШЗЕН0.1mЃЉ
ЃЈ1ЃЉЕБАкЩўOAгыOBГЩ45ЁуМаНЧЪБЃЌЧЁЮЊЖљЭЏЕФАВШЋИпЖШЃЌдђhЃНЁЁ ЁЁm
ЃЈ2ЃЉФГГЩШЫдкЭцЧяЧЇЪБЃЌАкЩўOCгыOBЕФзюДѓМаНЧЮЊ55ЁуЃЌЮЪДЫШЫЪЧЗёАВШЋЃПЃЈВЮПМЪ§ОнЃК![]() Ёж1.41ЃЌsin55ЁуЁж0.82ЃЌcos55ЁуЁж0.57ЃЌtan55ЁуЁж1.43ЃЉ
Ёж1.41ЃЌsin55ЁуЁж0.82ЃЌcos55ЁуЁж0.57ЃЌtan55ЁуЁж1.43ЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,![]() ЪЧ
ЪЧ![]() ЕФжаЯп,
ЕФжаЯп, ![]() ЪЧЩфЯп
ЪЧЩфЯп![]() ЩЯвЛЖЏЕу(ВЛгыЕу
ЩЯвЛЖЏЕу(ВЛгыЕу![]() жиКЯ).
жиКЯ).![]() НЛЩфЯп
НЛЩфЯп![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() ЃЌСЌНс
ЃЌСЌНс![]() .
.
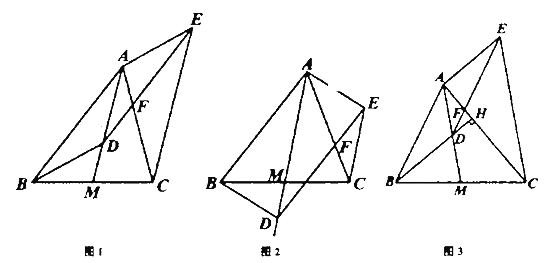
ЃЈ1ЃЉШчЭМ1,ЕБЕу![]() дк
дк![]() ЩЯЪБ,ЧѓжЄ:ЫФБпаЮ
ЩЯЪБ,ЧѓжЄ:ЫФБпаЮ![]() ЪЧЦНааЫФБпаЮЃЛ
ЪЧЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉШчЭМ2,ЕБЕу![]() дк
дк![]() ЩЯдЫЖЏЪБ,(1)жаЕФНсТлЛЙГЩСЂТ№?ЧыжБАДаДГіФуЕФНсТл;
ЩЯдЫЖЏЪБ,(1)жаЕФНсТлЛЙГЩСЂТ№?ЧыжБАДаДГіФуЕФНсТл;
ЃЈ3ЃЉШчЭМ3,бгГЄ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌШє
ЃЌШє![]() ,Чв
,Чв![]() ,ЧыЧѓГі
,ЧыЧѓГі![]() ЕФЖШЪ§.
ЕФЖШЪ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖдгкЦНУцжБНЧзјБъЯЕxOyжаЕФЕуPКЭЁбCЃЌИјГіШчЯТЖЈвхЃКШєЁбCЩЯДцдквЛИіЕуMЃЌЪЙЕУMPЃНMCЃЌдђГЦЕуPЮЊЁбCЕФЁАЕШОЖЕуЁБЃЌвбжЊЕуDЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌEЃЈ0ЃЌ2
ЃЉЃЌEЃЈ0ЃЌ2![]() ЃЉЃЌFЃЈЉ2ЃЌ0ЃЉЃЎ
ЃЉЃЌFЃЈЉ2ЃЌ0ЃЉЃЎ
ЃЈ1ЃЉЕБЁбOЕФАыОЖЮЊ1ЪБЃЌ
ЂйдкЕуDЃЌEЃЌFжаЃЌЁбOЕФЁАЕШОЖЕуЁБЪЧФФМИИіЕуЃЛ
ЂкзїжБЯпEFЃЌШєжБЯпEFЩЯЕФЕуTЃЈmЃЌnЃЉЪЧЁбOЕФЁАЕШОЖЕуЁБЃЌЧѓmЕФШЁжЕЗЖЮЇЃЎ
ЃЈ2ЃЉЙ§ЕуEзїEGЁЭEFНЛxжсгкЕуGЃЌШєЁїEFGИїБпЩЯЫљгаЕФЕуЖМЪЧФГИідВЕФЁАЕШОЖЕуЁБЃЌЧѓетИідВЕФАыОЖrЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com