
【题目】如图,![]() 是
是![]() 的中线,
的中线, ![]() 是射线
是射线![]() 上一动点(不与点
上一动点(不与点![]() 重合).
重合).![]() 交射线
交射线![]() 于点
于点![]() ,
,![]() ,连结
,连结![]() .
.
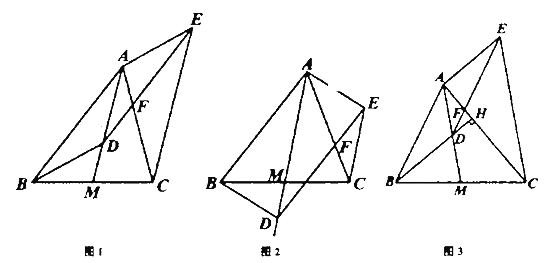
(1)如图1,当点![]() 在
在![]() 上时,求证:四边形
上时,求证:四边形![]() 是平行四边形;
是平行四边形;
(2)如图2,当点![]() 在
在![]() 上运动时,(1)中的结论还成立吗?请直按写出你的结论;
上运动时,(1)中的结论还成立吗?请直按写出你的结论;
(3)如图3,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,且
,且![]() ,请求出
,请求出![]() 的度数.
的度数.
【答案】(1)见解析;(2)成立;(3)![]() .
.
【解析】
(1)0根据平行线的性质可得四边形![]() 是平行四边形,则
是平行四边形,则![]() ,根据三角形中线的性质,全等三角形的判断和平行四边形的判定即可得到答案;
,根据三角形中线的性质,全等三角形的判断和平行四边形的判定即可得到答案;
(2)由(1)的证明过程可知,点![]() 在
在![]() 上任意位置,都有四边形
上任意位置,都有四边形![]() 是平行四边形;
是平行四边形;
(3)取线段![]() 的中点
的中点![]() ,连接
,连接![]() .根据三角形中位线定理和直角三角函数即可解答.
.根据三角形中位线定理和直角三角函数即可解答.
解:⑴证明:过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.
∵![]() ,∴四边形
,∴四边形![]() 是平行四边形,∴
是平行四边形,∴![]()
∵![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() 是
是![]() 的中线,∴
的中线,∴![]() ,
,
∴![]() ≌
≌![]() ,∴
,∴![]() ,
,
∴![]() .
.
∵![]() ,∴四边形
,∴四边形![]() 是平行四边形..Com]
是平行四边形..Com]
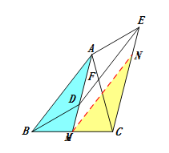
⑵结论:成立.
理由:由(1)的证明过程可知,点![]() 在
在![]() 上任意位置,都有四边形
上任意位置,都有四边形![]() 是平行四边形;
是平行四边形;
⑶如图,取线段![]() 的中点
的中点![]() ,连接
,连接![]() .
.
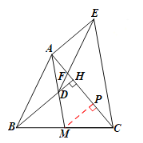
∵![]() ,∴
,∴![]() 是
是![]() 的中位线,
的中位线,
∴![]() ,
,![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]()
∵![]() ,∴
,∴![]() ,
,
![]() 中,∵
中,∵![]() ,∴
,∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A、B两点,与y轴交于点C,对称轴为直线x=-1,点B的坐标为(1,0),则下列结论:①AB=4;②b2-4ac>0;③ab<0;④a2-ab+ac<0,其中正确的结论有( )个.
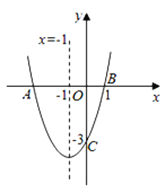
A. 3B. 4C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景
如图(1),在四边形ABCD中,∠B+∠D=180°,AB=AD,∠BAD=α,以点A为顶点作一个角,角的两边分别交BC,CD于点E,F,且∠EAF![]() α,连接EF,试探究:线段BE,DF,EF之间的数量关系.
α,连接EF,试探究:线段BE,DF,EF之间的数量关系.

(1)特殊情景
在上述条件下,小明增加条件“当∠BAD=∠B=∠D=90°时”如图(2),小明很快写出了:BE,DF,EF之间的数量关系为______.
(2)类比猜想
类比特殊情景,小明猜想:在如图(1)的条件下线段BE,DF,EF之间的数量关系是否仍然成立?若成立,请你帮助小明完成证明;若不成立,请说明理由.
(3)解决问题
如图(3),在△ABC中,∠BAC=90°,AB=AC=4,点D,E均在边BC上,且∠DAE=45°,若BD![]() ,请直接写出DE的长.
,请直接写出DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
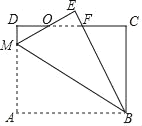
【题目】如图,在矩形ABCD中,AB=8,BC=6,M为AD上一点,将△ABM沿BM翻折至△EBM,ME和BE分别与CD相交于O,F两点,且OE=OD,则AM的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,边长为![]() 的正方形
的正方形![]() 的两顶点
的两顶点![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在原点.现将正方形
在原点.现将正方形![]() 绕
绕![]() 点顺时针旋转,
点顺时针旋转, ![]() 与
与![]() 轴相交于点
轴相交于点![]() ,如图,当
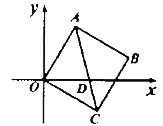
,如图,当![]() 时,点
时,点![]() 的坐标为( )
的坐标为( )
A. 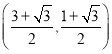 B.
B. 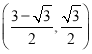 C.
C. 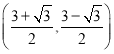 D.
D. 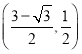
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系![]() 中,一组同心圆的圆心为坐标原点
中,一组同心圆的圆心为坐标原点![]() ,它们的半径分别为1,2,3,…,按照“加1”依次递增;一组平行线,
,它们的半径分别为1,2,3,…,按照“加1”依次递增;一组平行线,![]() ,
,![]() ,
,![]() ,
,![]() ,…都与x轴垂直,相邻两直线的间距为l,其中
,…都与x轴垂直,相邻两直线的间距为l,其中![]() 与
与![]() 轴重合若半径为2的圆与
轴重合若半径为2的圆与![]() 在第一象限内交于点
在第一象限内交于点![]() ,半径为3的圆与
,半径为3的圆与![]() 在第一象限内交于点
在第一象限内交于点![]() ,…,半径为
,…,半径为![]() 的圆与
的圆与![]() 在第一象限内交于点
在第一象限内交于点![]() ,则点
,则点![]() 的坐标为_____.(
的坐标为_____.(![]() 为正整数)
为正整数)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,禁止捕鱼期间,某海上稽查队在某海域巡逻,上午某一时刻在A处接到指挥部通知,在他们东北方向距离12海里的B处有一艘捕鱼船,正在沿南偏东75°方向以每小时10海里的速度航行,稽查队员立即乘坐巡逻船以每小时14海里的速度沿北偏东某一方向出发,在C处成功拦截捕鱼船,则巡逻船从出发到成功拦截捕鱼船所用的时间是( )

A. 1小时 B. 2小时 C. 3小时 D. 4小时
查看答案和解析>>
科目:初中数学 来源: 题型:
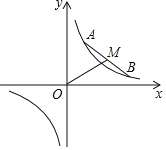
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() 在反比例函数
在反比例函数![]() 的图象上运动,且始终保持线段
的图象上运动,且始终保持线段![]() 的长度不变.
的长度不变.![]() 为线段
为线段![]() 的中点,连接
的中点,连接![]() .则线段
.则线段![]() 长度的最小值是_____(用含
长度的最小值是_____(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
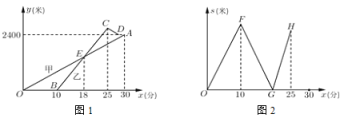
【题目】某校的甲、乙两位老师同住一小区,该小区与学校相距2400米. 甲从小区步行去学校,出发10分钟后乙再出发,乙从小区先骑公共自行车,途经学校义骑行若干米到达还车点后,立即步行走回学校. 已知甲步行的速度比乙步行的速度每分钟快5米. 设甲步行的时间为![]() (分),图1中线段
(分),图1中线段![]() 和折线
和折线![]() 分别表示甲、乙离开小区的路程
分别表示甲、乙离开小区的路程![]() (米)与甲步行时间
(米)与甲步行时间![]() (分)的函数关系的图象;图2表示甲、乙两人之间的距离
(分)的函数关系的图象;图2表示甲、乙两人之间的距离![]() (米)与甲步行时间
(米)与甲步行时间![]() (分)的函数关系的图象(不完整).根据图1和图2中所给信息,解答下列问题:
(分)的函数关系的图象(不完整).根据图1和图2中所给信息,解答下列问题:
(1)求甲步行的速度和乙出发时甲离开小区的路程;
(2)求乙骑自行车的速度和乙到达还车点时甲、乙两人之间的距离;
(3)在图2中,画出当![]() 时
时![]() 关于
关于![]() 的函数的大致图象. (温馨提示:请画在答题卷相对应的图上)
的函数的大致图象. (温馨提示:请画在答题卷相对应的图上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com