
【题目】如图,在矩形ABCD中,AB=8,BC=6,M为AD上一点,将△ABM沿BM翻折至△EBM,ME和BE分别与CD相交于O,F两点,且OE=OD,则AM的长为_____.
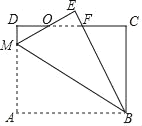
【答案】4.8
【解析】
根据矩形性质,证△ODP≌△OEG(ASA),DG=EP,运用勾股定理求AP.
如图所示:
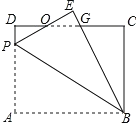
∵四边形ABCD是矩形,
∴∠D=∠A=∠C=90°,AD=BC=6,CD=AB=8,
根据题意得:△ABP≌△EBP,
∴EP=AP,∠E=∠A=90°,BE=AB=8,
在△ODP和△OEG中,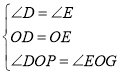 ,
,
∴△ODP≌△OEG(ASA),
∴OP=OG,PD=GE,
∴DG=EP,
设AP=EP=x,则PD=GE=6-x,DG=x,
∴CG=8-x,BG=8-(6-x)=2+x,
根据勾股定理得:BC2+CG2=BG2,
即62+(8-x)2=(x+2)2,
解得:x=4.8,
∴AP=4.8;
故答案为:4.8.


科目:初中数学 来源: 题型:
【题目】如图,抛物线与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 的坐标是
的坐标是![]() ,
,![]() 为抛物线上的一个动点,过点
为抛物线上的一个动点,过点![]() 作
作![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,抛物线的对称轴是直线
,抛物线的对称轴是直线![]() .
.
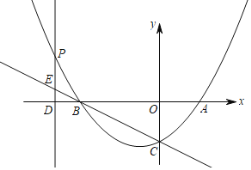
(1)求抛物线的函数表达式;
(2)若点![]() 在第二象限内,且
在第二象限内,且![]() ,求
,求![]() 的面积.
的面积.
(3)在(2)的条件下,若![]() 为直线
为直线![]() 上一点,在
上一点,在![]() 轴的下方,是否存在点
轴的下方,是否存在点![]() ,使
,使![]() 是以
是以![]() 为腰的等腰三角形?若存在,求出点
为腰的等腰三角形?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 为顺利通过“国家文明城市”验收,市政府拟对城区部分路段的人行道地砖、绿化带、排水管等公用设施全面更新改造,现有甲、乙两个工程队有意承包这项工程,经调查知道,乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的2倍,若甲、乙两工程队合作只需10天完成.甲、乙两个工程队单独完成此项工程各需多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全面两孩政策实施后,甲,乙两个家庭有了各自的规划.假定生男生女的概率相同,回答下列问题:
(1)甲家庭已有一个男孩,准备再生一个孩子,则第二个孩子是女孩的概率是 ;
(2)乙家庭没有孩子,准备生两个孩子,求至少有一个孩子是女孩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某新农村乐园设置了一个秋千场所,如图所示,秋千拉绳OB的长为3m,静止时,踏板到地面距离BD的长为0.6m(踏板厚度忽略不计).为安全起见,乐园管理处规定:儿童的“安全高度”为hm,成人的“安全高度”为2m(计算结果精确到0.1m)
(1)当摆绳OA与OB成45°夹角时,恰为儿童的安全高度,则h= m
(2)某成人在玩秋千时,摆绳OC与OB的最大夹角为55°,问此人是否安全?(参考数据:![]() ≈1.41,sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
≈1.41,sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程对承接了60万平方米的绿化工程,由于情况有变,……,设原计划每天绿化的面积为![]() 万平方米,列方程为
万平方米,列方程为![]() ,根据方程可知省略的部分是( )
,根据方程可知省略的部分是( )
A.实际工作时每天的工作效率比原计划提高了20%,结果提前30天完成了这一任务
B.实际工作时每天的工作效率比原计划提高了20%,结果延误30天完成了这一任务
C.实际工作时每天的工作效率比原计划降低了20%,结果延误30天完成了这一任务
D.实际工作时每天的工作效率比原计划降低了20%,结果提前30天完成了这一任务
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的中线,
的中线, ![]() 是射线
是射线![]() 上一动点(不与点
上一动点(不与点![]() 重合).
重合).![]() 交射线
交射线![]() 于点
于点![]() ,
,![]() ,连结
,连结![]() .
.
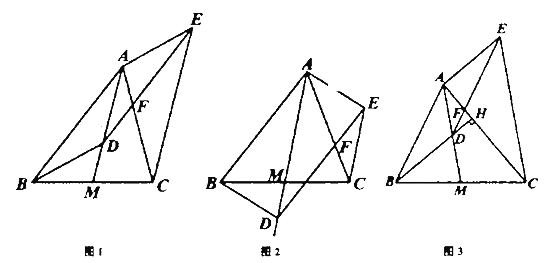
(1)如图1,当点![]() 在
在![]() 上时,求证:四边形
上时,求证:四边形![]() 是平行四边形;
是平行四边形;
(2)如图2,当点![]() 在
在![]() 上运动时,(1)中的结论还成立吗?请直按写出你的结论;
上运动时,(1)中的结论还成立吗?请直按写出你的结论;
(3)如图3,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,且
,且![]() ,请求出
,请求出![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张前往某精密仪器厂应聘,公司承诺工资待遇如下.
工资待遇:每月工资至少3000元,每天工作8小时,每月工作25天,加工1件![]() 型零件计酬16元,加工1件
型零件计酬16元,加工1件![]() 型零件计酬12元,月工资
型零件计酬12元,月工资![]() 底薪(800元)
底薪(800元)![]() 计件工资 .
计件工资 .
进厂后小张发现:加工1件![]() 型零件和3件
型零件和3件![]() 型零件需要5小时;加工2件
型零件需要5小时;加工2件![]() 型零件和5件
型零件和5件![]() 型零件需9小时.
型零件需9小时.
(1)小张加工1件![]() 型零件和1件
型零件和1件![]() 型零件各需要多少小时?
型零件各需要多少小时?
(2)若公司规定:小张每月必须加工![]() 两种型号的零件,且加工
两种型号的零件,且加工![]() 型的数量不大于
型的数量不大于![]() 型零件数量的2倍,设小张每月加工
型零件数量的2倍,设小张每月加工![]() 零件
零件![]() 件,工资总额为
件,工资总额为![]() 元,请你运用所学知识判断该公司颁布执行此规定后是否违背了工资待遇承诺?
元,请你运用所学知识判断该公司颁布执行此规定后是否违背了工资待遇承诺?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() .
.
(Ⅰ)当抛物线经过点![]() 时,求抛物线的顶点坐标;
时,求抛物线的顶点坐标;
(Ⅱ)若该抛物线开口向上,当![]() 时,抛物线的最高点为
时,抛物线的最高点为![]() ,最低点为
,最低点为![]() ,点
,点![]() 的纵坐标为
的纵坐标为![]() ,求点
,求点![]() 和点
和点![]() 的坐标。
的坐标。
(Ⅲ)点![]() ,
,![]() 为抛物线上的两点,设
为抛物线上的两点,设![]() ,当
,当![]() 时,均有
时,均有![]() ,求
,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com