
【题目】已知抛物线![]() .
.
(Ⅰ)当抛物线经过点![]() 时,求抛物线的顶点坐标;
时,求抛物线的顶点坐标;
(Ⅱ)若该抛物线开口向上,当![]() 时,抛物线的最高点为
时,抛物线的最高点为![]() ,最低点为
,最低点为![]() ,点
,点![]() 的纵坐标为
的纵坐标为![]() ,求点
,求点![]() 和点
和点![]() 的坐标。
的坐标。
(Ⅲ)点![]() ,
,![]() 为抛物线上的两点,设
为抛物线上的两点,设![]() ,当
,当![]() 时,均有
时,均有![]() ,求
,求![]() 的取值范围。
的取值范围。
【答案】(Ⅰ)![]() ;(Ⅱ)点
;(Ⅱ)点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ;(Ⅲ)
;(Ⅲ)![]() 的取值范围是
的取值范围是![]() .
.
【解析】
(Ⅰ)把点![]() 代入
代入![]() 中,得到关于a的方程,解方程求出a的值,从而确定抛物线的解析式,即可求出抛物线的顶点坐标;
中,得到关于a的方程,解方程求出a的值,从而确定抛物线的解析式,即可求出抛物线的顶点坐标;
(Ⅱ)先求出抛物线的对称轴,再根据二次函数的图像和自变量的取值范围确定y的最大值和最小值,再根据抛物线的最高点为![]() 的纵坐标为
的纵坐标为![]() ,求出a的值,从而确定点M、 N的坐标.
,求出a的值,从而确定点M、 N的坐标.
(Ⅲ)当t≤x1≤t+1,x2≥3时,均满足y1≥y2,推出抛物线开口向下,找出x=3时的对称点为x=-1, 结合函数图像可得:![]() t+1≤3,由此即可解决问题;
t+1≤3,由此即可解决问题;
解:(Ⅰ)∵抛物线经过![]() ,∴
,∴![]() ,解得
,解得![]() .
.
∴抛物线的解析式为![]() .
.
∵![]() ,∴抛物线的顶点坐标为
,∴抛物线的顶点坐标为![]() .
.
(Ⅱ)抛物线的对称轴为直线![]() .
.
∵抛物线开口向上,
∴当![]() 时,
时,![]() 随
随![]() 的增大而减小;
的增大而减小;
当![]() 时,
时,![]() 随
随![]() 的增大而增大.
的增大而增大.
∴当![]() 时,
时,![]() 取得最大值;当
取得最大值;当![]() 时,
时,![]() 取得最小值.
取得最小值.
由![]() ,解得
,解得![]() .
.
当![]() 时,
时,![]() .
.
∴点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(Ⅲ)当![]() 时,不合题意,∴
时,不合题意,∴![]() .
.
由![]() ,解得
,解得![]() 或
或![]() .
.
由![]() ,解得
,解得![]() .
.
∴![]() 的取值范围是
的取值范围是![]() .
.


 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:初中数学 来源: 题型:
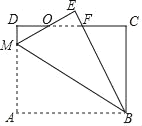
【题目】如图,在矩形ABCD中,AB=8,BC=6,M为AD上一点,将△ABM沿BM翻折至△EBM,ME和BE分别与CD相交于O,F两点,且OE=OD,则AM的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
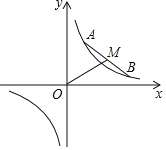
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() 在反比例函数
在反比例函数![]() 的图象上运动,且始终保持线段
的图象上运动,且始终保持线段![]() 的长度不变.
的长度不变.![]() 为线段
为线段![]() 的中点,连接
的中点,连接![]() .则线段
.则线段![]() 长度的最小值是_____(用含
长度的最小值是_____(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
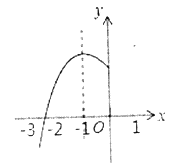
【题目】已知抛物线![]() 的对称轴为
的对称轴为![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() 和
和![]() 之间,其部分图像如图所示,则下列结论:①点
之间,其部分图像如图所示,则下列结论:①点![]() ,
,![]() ,
,![]() 是该抛物线上的点,则
是该抛物线上的点,则![]() ;②
;②![]() ;③
;③![]() (
(![]() 为任意实数).其中正确结论的个数是( )
为任意实数).其中正确结论的个数是( )
A. 0B. 1C. 2D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的最大值为4,且该抛物线与
的最大值为4,且该抛物线与![]() 轴的交点为
轴的交点为![]() ,顶点为
,顶点为![]() .
.
(1)求该二次函数的解析式及点![]() ,
,![]() 的坐标;
的坐标;
(2)点![]() 是
是![]() 轴上的动点,
轴上的动点,
①求![]() 的最大值及对应的点
的最大值及对应的点![]() 的坐标;
的坐标;
②设![]() 是
是![]() 轴上的动点,若线段
轴上的动点,若线段![]() 与函数
与函数![]() 的图像只有一个公共点,求
的图像只有一个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
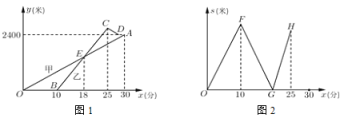
【题目】某校的甲、乙两位老师同住一小区,该小区与学校相距2400米. 甲从小区步行去学校,出发10分钟后乙再出发,乙从小区先骑公共自行车,途经学校义骑行若干米到达还车点后,立即步行走回学校. 已知甲步行的速度比乙步行的速度每分钟快5米. 设甲步行的时间为![]() (分),图1中线段
(分),图1中线段![]() 和折线
和折线![]() 分别表示甲、乙离开小区的路程
分别表示甲、乙离开小区的路程![]() (米)与甲步行时间
(米)与甲步行时间![]() (分)的函数关系的图象;图2表示甲、乙两人之间的距离
(分)的函数关系的图象;图2表示甲、乙两人之间的距离![]() (米)与甲步行时间
(米)与甲步行时间![]() (分)的函数关系的图象(不完整).根据图1和图2中所给信息,解答下列问题:
(分)的函数关系的图象(不完整).根据图1和图2中所给信息,解答下列问题:
(1)求甲步行的速度和乙出发时甲离开小区的路程;
(2)求乙骑自行车的速度和乙到达还车点时甲、乙两人之间的距离;
(3)在图2中,画出当![]() 时
时![]() 关于
关于![]() 的函数的大致图象. (温馨提示:请画在答题卷相对应的图上)
的函数的大致图象. (温馨提示:请画在答题卷相对应的图上)
查看答案和解析>>
科目:初中数学 来源: 题型:
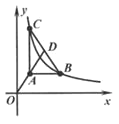
【题目】如图,在直角坐标系中,O为坐标原点,点A(1,2),过点A分别作x轴、y轴的平行线交反比例函数y=![]() (x>0)的图象于点B,C,延长OA交BC于点D.若△ABD的面积为2,则k的值为______.
(x>0)的图象于点B,C,延长OA交BC于点D.若△ABD的面积为2,则k的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着粤港澳大湾区建设的加速推进,广东省正加速布局以5G等为代表的战略性新兴产业,据统计,目前广东5G基站的数量约1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座。
(1)计划到2020年底,全省5G基站的数量是多少万座?;
(2)按照计划,求2020年底到2022年底,全省5G基站数量的年平均增长率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com