
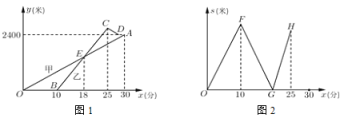
【题目】某校的甲、乙两位老师同住一小区,该小区与学校相距2400米. 甲从小区步行去学校,出发10分钟后乙再出发,乙从小区先骑公共自行车,途经学校义骑行若干米到达还车点后,立即步行走回学校. 已知甲步行的速度比乙步行的速度每分钟快5米. 设甲步行的时间为![]() (分),图1中线段
(分),图1中线段![]() 和折线
和折线![]() 分别表示甲、乙离开小区的路程
分别表示甲、乙离开小区的路程![]() (米)与甲步行时间
(米)与甲步行时间![]() (分)的函数关系的图象;图2表示甲、乙两人之间的距离
(分)的函数关系的图象;图2表示甲、乙两人之间的距离![]() (米)与甲步行时间
(米)与甲步行时间![]() (分)的函数关系的图象(不完整).根据图1和图2中所给信息,解答下列问题:
(分)的函数关系的图象(不完整).根据图1和图2中所给信息,解答下列问题:
(1)求甲步行的速度和乙出发时甲离开小区的路程;
(2)求乙骑自行车的速度和乙到达还车点时甲、乙两人之间的距离;
(3)在图2中,画出当![]() 时
时![]() 关于
关于![]() 的函数的大致图象. (温馨提示:请画在答题卷相对应的图上)
的函数的大致图象. (温馨提示:请画在答题卷相对应的图上)
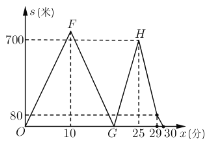
【答案】(1)甲步行的速度是80 米/分,乙出发时甲离开小区的路程是800 米;(2)乙到达还车点时,甲、乙两人之间的距离是700 米;(3)图象如图所示见解析.
【解析】
(1)根据函数图象中的数据可以求得甲步行的速度和乙出发时甲离开小区的路程;
(2)根据函数图象中的数据可以求得OA的函数解析式,然后将x=18代入OA的函数解析式,即可求得点E的纵坐标,进而可以求得乙骑自行车的速度和乙到达还车点时甲、乙两人之间的距离;
(3)根据题意可以求得乙到达学校的时间,从而可以函数图象补充完整.
(1)由题意,得:甲步行的速度是![]() (米/分),
(米/分),
∴乙出发时甲离开小区的路程是![]() (米).
(米).
(2)设直线![]() 的解析式为:
的解析式为:![]() ,
,
∵直线![]() 过点
过点![]() ,
,
∴![]() ,
,
解得![]() ,
,
∴直线![]() 的解析式为:
的解析式为:![]() .
.
∴当![]() 时,
时,![]() ,
,
∴乙骑自行车的速度是![]() (米/分).
(米/分).
∵乙骑自行车的时间为![]() (分),
(分),
∴乙骑自行车的路程为![]() (米).
(米).
当![]() 时,甲走过的路程是
时,甲走过的路程是![]() (米),
(米),
∴乙到达还车点时,甲、乙两人之间的距离是![]() (米).
(米).
(3)乙步行的速度为:80-5=75(米/分),
乙到达学校用的时间为:25+(2700-2400)÷75=29(分),
当25≤x≤30时s关于x的函数的大致图象如图所示.


科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的中线,
的中线, ![]() 是射线
是射线![]() 上一动点(不与点
上一动点(不与点![]() 重合).
重合).![]() 交射线
交射线![]() 于点
于点![]() ,
,![]() ,连结
,连结![]() .
.
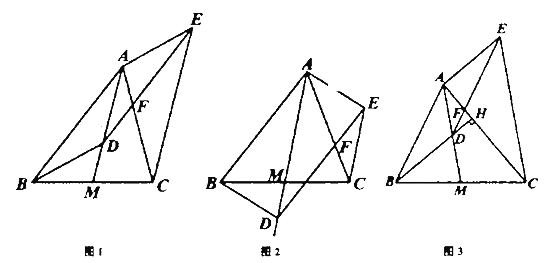
(1)如图1,当点![]() 在
在![]() 上时,求证:四边形
上时,求证:四边形![]() 是平行四边形;
是平行四边形;
(2)如图2,当点![]() 在
在![]() 上运动时,(1)中的结论还成立吗?请直按写出你的结论;
上运动时,(1)中的结论还成立吗?请直按写出你的结论;
(3)如图3,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,且
,且![]() ,请求出
,请求出![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若⊙C上存在一个点M,使得MP=MC,则称点P为⊙C的“等径点”,已知点D(![]() ,
,![]() ),E(0,2
),E(0,2![]() ),F(﹣2,0).
),F(﹣2,0).
(1)当⊙O的半径为1时,
①在点D,E,F中,⊙O的“等径点”是哪几个点;
②作直线EF,若直线EF上的点T(m,n)是⊙O的“等径点”,求m的取值范围.
(2)过点E作EG⊥EF交x轴于点G,若△EFG各边上所有的点都是某个圆的“等径点”,求这个圆的半径r的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() .
.
(Ⅰ)当抛物线经过点![]() 时,求抛物线的顶点坐标;
时,求抛物线的顶点坐标;
(Ⅱ)若该抛物线开口向上,当![]() 时,抛物线的最高点为
时,抛物线的最高点为![]() ,最低点为
,最低点为![]() ,点
,点![]() 的纵坐标为
的纵坐标为![]() ,求点
,求点![]() 和点
和点![]() 的坐标。
的坐标。
(Ⅲ)点![]() ,
,![]() 为抛物线上的两点,设
为抛物线上的两点,设![]() ,当
,当![]() 时,均有
时,均有![]() ,求
,求![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.
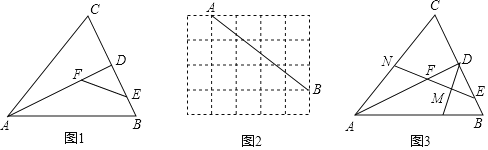
(1)如图1,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点.求证:四边形
上的点.求证:四边形![]() 是邻余四边形.
是邻余四边形.
(2)如图2,在![]() 的方格纸中,
的方格纸中,![]() ,
,![]() 在格点上,请画出一个符合条件的邻余四边形
在格点上,请画出一个符合条件的邻余四边形![]() ,使
,使![]() 是邻余线,
是邻余线,![]() ,
,![]() 在格点上.
在格点上.
(3)如图3,在(1)的条件下,取![]() 中点
中点![]() ,连结
,连结![]() 并延长交
并延长交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .若
.若![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() ,求邻余线
,求邻余线![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随机抽取某小吃店一周的营业额(单位:元)如下表:
星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 | 合计 |
540 | 680 | 640 | 640 | 780 | 1110 | 1070 | 5460 |
(1)分析数据,填空:这组数据的平均数是 元,中位数是 元,众数是 元.
(2)估计一个月的营业额(按30天计算):
①星期一到星期五营业额相差不大,用这5天的平均数估算合适么: .(填“合适”或“不合适”)
②选择一个你认为最合适的数据估算这个小吃店一个月的营业额.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一辆超市购物车放置在水平地面上,其侧面四边形ABCD与地面某条水平线l在同一平面内,且AB∥l,若∠A=93°,∠D=111°,则直线CD与l所夹锐角的度数为( )

A. 15°B. 18°C. 21°D. 24°
查看答案和解析>>
科目:初中数学 来源: 题型:
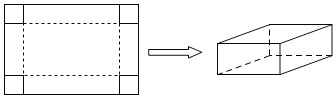
【题目】如图,工人师傅用一块长为10分米,宽为6分米的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形;(厚度不计)
(1)当长方体底面面积为12平方分米时,裁掉的正方形边长为______分米;
(2)若要求制作的长方体的底面长不大于底面宽的5倍,且将容器的外表面进行防锈处理,其侧面处理费用为0.5元/平方分米,底面处理费用为2元/平方分米;求:裁掉的正方形边长为多大时,防锈处理总费用最低,最低为多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com