
【题目】定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.
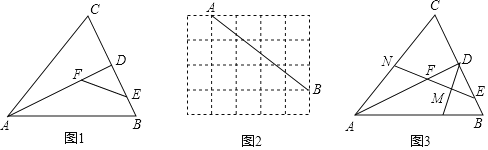
(1)如图1,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点.求证:四边形
上的点.求证:四边形![]() 是邻余四边形.
是邻余四边形.
(2)如图2,在![]() 的方格纸中,
的方格纸中,![]() ,
,![]() 在格点上,请画出一个符合条件的邻余四边形
在格点上,请画出一个符合条件的邻余四边形![]() ,使
,使![]() 是邻余线,
是邻余线,![]() ,
,![]() 在格点上.
在格点上.
(3)如图3,在(1)的条件下,取![]() 中点
中点![]() ,连结
,连结![]() 并延长交
并延长交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .若
.若![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() ,求邻余线
,求邻余线![]() 的长.
的长.
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,边长为![]() 的正方形
的正方形![]() 的两顶点
的两顶点![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在原点.现将正方形
在原点.现将正方形![]() 绕
绕![]() 点顺时针旋转,
点顺时针旋转, ![]() 与
与![]() 轴相交于点
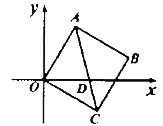
轴相交于点![]() ,如图,当
,如图,当![]() 时,点
时,点![]() 的坐标为( )
的坐标为( )
A. 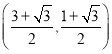 B.
B. 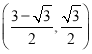 C.
C. 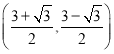 D.
D. 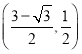
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的最大值为4,且该抛物线与
的最大值为4,且该抛物线与![]() 轴的交点为
轴的交点为![]() ,顶点为
,顶点为![]() .
.
(1)求该二次函数的解析式及点![]() ,
,![]() 的坐标;
的坐标;
(2)点![]() 是
是![]() 轴上的动点,
轴上的动点,
①求![]() 的最大值及对应的点
的最大值及对应的点![]() 的坐标;
的坐标;
②设![]() 是
是![]() 轴上的动点,若线段
轴上的动点,若线段![]() 与函数
与函数![]() 的图像只有一个公共点,求
的图像只有一个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
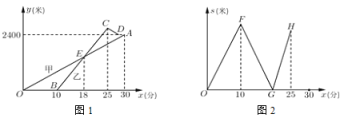
【题目】某校的甲、乙两位老师同住一小区,该小区与学校相距2400米. 甲从小区步行去学校,出发10分钟后乙再出发,乙从小区先骑公共自行车,途经学校义骑行若干米到达还车点后,立即步行走回学校. 已知甲步行的速度比乙步行的速度每分钟快5米. 设甲步行的时间为![]() (分),图1中线段
(分),图1中线段![]() 和折线
和折线![]() 分别表示甲、乙离开小区的路程
分别表示甲、乙离开小区的路程![]() (米)与甲步行时间
(米)与甲步行时间![]() (分)的函数关系的图象;图2表示甲、乙两人之间的距离
(分)的函数关系的图象;图2表示甲、乙两人之间的距离![]() (米)与甲步行时间
(米)与甲步行时间![]() (分)的函数关系的图象(不完整).根据图1和图2中所给信息,解答下列问题:
(分)的函数关系的图象(不完整).根据图1和图2中所给信息,解答下列问题:
(1)求甲步行的速度和乙出发时甲离开小区的路程;
(2)求乙骑自行车的速度和乙到达还车点时甲、乙两人之间的距离;
(3)在图2中,画出当![]() 时
时![]() 关于
关于![]() 的函数的大致图象. (温馨提示:请画在答题卷相对应的图上)
的函数的大致图象. (温馨提示:请画在答题卷相对应的图上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】箭头四角形,模型规律:如图1,延长CO交AB于点D,则![]() .因为凹四边形ABOC形似箭头,其四角具有“
.因为凹四边形ABOC形似箭头,其四角具有“![]() ”这个规律,所以我们把这个模型叫做“箭头四角形”.模型应用:
”这个规律,所以我们把这个模型叫做“箭头四角形”.模型应用:
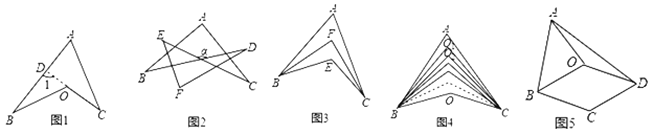
(1)直接应用:
①如图2,![]() .
.
②如图3,![]() 的2等分线(即角平分线)
的2等分线(即角平分线)![]() 交于点F,已知
交于点F,已知![]() ,则
,则![]()
③如图4,![]() 分别为
分别为![]() 的2019等分线
的2019等分线![]() .它们的交点从上到下依次为
.它们的交点从上到下依次为![]() .已知
.已知![]() ,则
,则![]() 度
度
(2)拓展应用:如图5,在四边形ABCD中,![]() .O是四边形ABCD内一点,且
.O是四边形ABCD内一点,且![]() .求证:四边形OBCD是菱形.
.求证:四边形OBCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级全体男生1000米跑步的成绩,随机抽取了部分男生进行测试,并将测试成绩分为![]() 、
、![]() 、
、![]() 、
、![]() 四个等级,绘制如下不完整的统计图表,如题图表所示,根据图表信息解答下列问题:
四个等级,绘制如下不完整的统计图表,如题图表所示,根据图表信息解答下列问题:
成绩等级频数分布表
成绩等级 | 频数 |
A | 24 |
B | 10 |
C | x |
D | 2 |
合计 | y |
成绩等级扇形统计图

(1)x=______,y=______,扇形图中表示![]() 的圆心角的度数为______度;
的圆心角的度数为______度;
(2)甲、乙、丙是![]() 等级中的三名学生,学校决定从这三名学生中随机抽取两名介绍体育锻炼经验,用列表法或画树状图法,求同时抽到甲、乙两名学生的概率.
等级中的三名学生,学校决定从这三名学生中随机抽取两名介绍体育锻炼经验,用列表法或画树状图法,求同时抽到甲、乙两名学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顶点为![]() 的二次函数图象与x轴交于点
的二次函数图象与x轴交于点![]() ,点B在该图象上,
,点B在该图象上,![]() 交其对称轴l于点M,点M、N关于点P对称,连接
交其对称轴l于点M,点M、N关于点P对称,连接![]() 、
、![]() .
.
(1)求该二次函数的关系式.
(2)若点B在对称轴l右侧的二次函数图象上运动,请解答下列问题:
①连接![]() ,当
,当![]() 时,请判断
时,请判断![]() 的形状,并求出此时点B的坐标.
的形状,并求出此时点B的坐标.
②求证:![]() .
.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com