
【题目】如图,顶点为![]() 的二次函数图象与x轴交于点
的二次函数图象与x轴交于点![]() ,点B在该图象上,
,点B在该图象上,![]() 交其对称轴l于点M,点M、N关于点P对称,连接
交其对称轴l于点M,点M、N关于点P对称,连接![]() 、
、![]() .
.
(1)求该二次函数的关系式.
(2)若点B在对称轴l右侧的二次函数图象上运动,请解答下列问题:
①连接![]() ,当
,当![]() 时,请判断
时,请判断![]() 的形状,并求出此时点B的坐标.
的形状,并求出此时点B的坐标.
②求证:![]() .
.

【答案】(1)二次函数的关系式为![]() ;(2)①
;(2)①![]() 是等腰直角三角形,此时点B坐标为
是等腰直角三角形,此时点B坐标为![]() ;②见解析
;②见解析
【解析】
(1)利用待定系数法即可得到答案;
(2)①设![]() ,由点的对称性得到
,由点的对称性得到![]() ,再由勾股定理得到答案;②设直线
,再由勾股定理得到答案;②设直线![]() 与x轴交于点D,求得直线
与x轴交于点D,求得直线![]() 解析式,再结合题意即可得到答案.
解析式,再结合题意即可得到答案.
解:(1)∵二次函数顶点为![]()
∴设顶点式![]()
∵二次函数图象过点![]()
∴![]() ,解得:
,解得:![]()
∴二次函数的关系式为![]()
(2)设![]()
∴直线![]() 解析式为:
解析式为:![]()
∵![]() 交对称轴l于点M
交对称轴l于点M
∴当![]() 时,
时,![]()
∴![]()
∵点M、N关于点P对称
∴![]() ,
,
∴![]() ,即
,即![]()
①∵![]()
∴![]()
∴![]()
解得:![]()
∴![]()
∴![]() ,
,![]()
∴![]() ,
,![]() ,B
,B![]()
∴![]() ,
,![]()
∴![]() 是等腰直角三角形,此时点B坐标为
是等腰直角三角形,此时点B坐标为![]() .
.
②证明:如图,设直线![]() 与x轴交于点D
与x轴交于点D
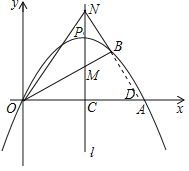
∵![]() 、
、![]()
设直线![]() 解析式为
解析式为![]()
∴ 解得:
解得:
∴直线![]() :
:![]()
当![]() 时,
时,![]() ,解得:
,解得:![]()
∴![]()
∵![]() ,
,![]() 轴
轴
∴![]() 垂直平分
垂直平分![]()
∴![]()
∴![]()


科目:初中数学 来源: 题型:
【题目】定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.
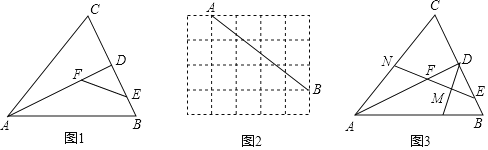
(1)如图1,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点.求证:四边形
上的点.求证:四边形![]() 是邻余四边形.
是邻余四边形.
(2)如图2,在![]() 的方格纸中,
的方格纸中,![]() ,
,![]() 在格点上,请画出一个符合条件的邻余四边形
在格点上,请画出一个符合条件的邻余四边形![]() ,使
,使![]() 是邻余线,
是邻余线,![]() ,
,![]() 在格点上.
在格点上.
(3)如图3,在(1)的条件下,取![]() 中点
中点![]() ,连结
,连结![]() 并延长交
并延长交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .若
.若![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() ,求邻余线
,求邻余线![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,解答问题:
为解方程![]() ,我们可以将
,我们可以将![]() 视为一个整体,然后设
视为一个整体,然后设![]() ,则
,则![]() ,原方程可化为
,原方程可化为![]() ,解此方程得
,解此方程得![]() .当
.当![]() 时,
时,![]() ,∴
,∴![]() ;当
;当![]() 时,
时,![]() ,∴
,∴![]() ,∴原方程的解为
,∴原方程的解为![]() .
.
(1)填空:在原方程得到方程(*)的过程中,利用________法达到了降次的目的,体现了________的数学思想;
(2)解方程:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
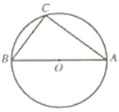
【题目】如图,⊙O的直径AB=10,弦AC=8,连接BC。
(1)尺规作图:作弦CD,使CD=BC(点D不与B重合),连接AD;(保留作图痕迹,不写作法)
(2)在(1)所作的图中,求四边形ABCD的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
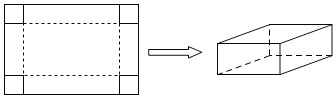
【题目】如图,工人师傅用一块长为10分米,宽为6分米的矩形铁皮制作一个无盖的长方体容器,需要将四角各裁掉一个正方形;(厚度不计)
(1)当长方体底面面积为12平方分米时,裁掉的正方形边长为______分米;
(2)若要求制作的长方体的底面长不大于底面宽的5倍,且将容器的外表面进行防锈处理,其侧面处理费用为0.5元/平方分米,底面处理费用为2元/平方分米;求:裁掉的正方形边长为多大时,防锈处理总费用最低,最低为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
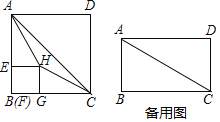
【题目】在矩形![]() 中,连结
中,连结![]() ,点E从点B出发,以每秒1个单位的速度沿着
,点E从点B出发,以每秒1个单位的速度沿着![]() 的路径运动,运动时间为t(秒).过点E作
的路径运动,运动时间为t(秒).过点E作![]() 于点F,在矩形
于点F,在矩形![]() 的内部作正方形
的内部作正方形![]() .
.
(1)如图,当![]() 时,
时,
①若点H在![]() 的内部,连结
的内部,连结![]() 、
、![]() ,求证:
,求证:![]() ;
;
②当![]() 时,设正方形
时,设正方形![]() 与
与![]() 的重叠部分面积为S,求S与t的函数关系式;
的重叠部分面积为S,求S与t的函数关系式;
(2)当![]() ,
,![]() 时,若直线
时,若直线![]() 将矩形
将矩形![]() 的面积分成1︰3两部分,求t的值.
的面积分成1︰3两部分,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《如果想毁掉一个孩子,就给他一部手机!》这是2017年微信圈一篇热传的文章.国际上,法国教育部宣布从 2018 年9月新学期起小学和初中禁止学生使用手机.为了解学生手机使用情况,某学校开展了“手机伴我健康行”主题活动,他们随机抽取部分学生进行“使用手机目的”和“每周使用手机的时间”的问卷调查,并绘制成如图①,②的 统计图,已知“查资料”的人数是 40人.请你根据以上信息解答下列问题:
(1)在扇形统计图中,“玩游戏”对应的百分比为______,圆心角度数是______度;
(2)补全条形统计图;
(3)该校共有学生2100人,估计每周使用手机时间在2 小时以上(不含2小时)的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com