
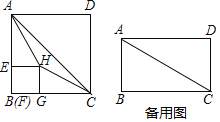
【题目】在矩形![]() 中,连结
中,连结![]() ,点E从点B出发,以每秒1个单位的速度沿着
,点E从点B出发,以每秒1个单位的速度沿着![]() 的路径运动,运动时间为t(秒).过点E作
的路径运动,运动时间为t(秒).过点E作![]() 于点F,在矩形
于点F,在矩形![]() 的内部作正方形
的内部作正方形![]() .
.
(1)如图,当![]() 时,
时,
①若点H在![]() 的内部,连结
的内部,连结![]() 、
、![]() ,求证:
,求证:![]() ;
;
②当![]() 时,设正方形
时,设正方形![]() 与
与![]() 的重叠部分面积为S,求S与t的函数关系式;
的重叠部分面积为S,求S与t的函数关系式;
(2)当![]() ,
,![]() 时,若直线
时,若直线![]() 将矩形
将矩形![]() 的面积分成1︰3两部分,求t的值.
的面积分成1︰3两部分,求t的值.
【答案】(1)①证明见解析;②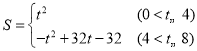 ;(3)t的值为
;(3)t的值为![]() 或
或![]() 或
或![]() .
.
【解析】
(1)①如图1中,证明![]() 即可解决问题.
即可解决问题.
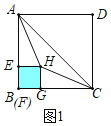
②分两种情形分别求解:如图1中,当![]() 时,重叠部分是正方形
时,重叠部分是正方形![]() .如图2中,当
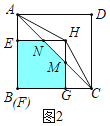
.如图2中,当![]() 时,重叠部分是五边形
时,重叠部分是五边形![]() .
.
(2)分三种情形分别求解:①如图3﹣1中,延长![]() 交
交![]() 于M,当
于M,当![]() 时,直线
时,直线![]() 将矩形
将矩形![]() 的面积分成1︰3两部分.②如图3﹣2中,延长
的面积分成1︰3两部分.②如图3﹣2中,延长![]() 交
交![]() 于M交
于M交![]() 的延长线于K,当
的延长线于K,当![]() 时,直线
时,直线![]() 将矩形
将矩形![]() 的面积分成1︰3两部分.③如图3﹣3中,当点E在线段
的面积分成1︰3两部分.③如图3﹣3中,当点E在线段![]() 上时,延长
上时,延长![]() 交
交![]() 于M,交
于M,交![]() 的延长线于N.当
的延长线于N.当![]() 时,直线
时,直线![]() 将矩形
将矩形![]() 的面积分成1︰3两部分.
的面积分成1︰3两部分.
解:(1)①如图1中,
∵四边形![]() 是正方形,
是正方形,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
②如图1中,当![]() 时,重叠部分是正方形
时,重叠部分是正方形![]() ,
,![]() .
.
如图2中,当![]() 时,重叠部分是五边形
时,重叠部分是五边形![]() ,
,![]() .
.
综上所述,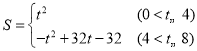 .
.
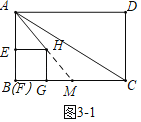
(2)如图3﹣1中,延长![]() 交
交![]() 于M,当
于M,当![]() 时,直线
时,直线![]() 将矩形
将矩形![]() 的面积分成1︰3两部分.
的面积分成1︰3两部分.
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
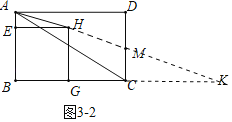
如图3﹣2中,延长![]() 交
交![]() 于M交
于M交![]() 的延长线于K,当
的延长线于K,当![]() 时,直线
时,直线![]() 将矩形
将矩形![]() 的面积分成1︰3两部分,易证
的面积分成1︰3两部分,易证![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
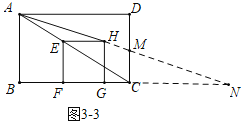
如图3﹣3中,当点E在线段![]() 上时,延长
上时,延长![]() 交
交![]() 于M,交
于M,交![]() 的延长线于N.当
的延长线于N.当![]() 时,直线
时,直线![]() 将矩形
将矩形![]() 的面积分成1︰3两部分,易证
的面积分成1︰3两部分,易证![]() .
.
在![]() 中,
中,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴ ,
,
解得![]() .
.
综上所述,满足条件的t的值为![]() 或
或![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】箭头四角形,模型规律:如图1,延长CO交AB于点D,则![]() .因为凹四边形ABOC形似箭头,其四角具有“
.因为凹四边形ABOC形似箭头,其四角具有“![]() ”这个规律,所以我们把这个模型叫做“箭头四角形”.模型应用:
”这个规律,所以我们把这个模型叫做“箭头四角形”.模型应用:
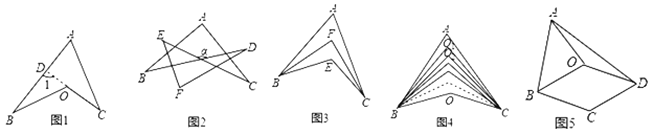
(1)直接应用:
①如图2,![]() .
.
②如图3,![]() 的2等分线(即角平分线)
的2等分线(即角平分线)![]() 交于点F,已知
交于点F,已知![]() ,则
,则![]()
③如图4,![]() 分别为
分别为![]() 的2019等分线
的2019等分线![]() .它们的交点从上到下依次为
.它们的交点从上到下依次为![]() .已知
.已知![]() ,则
,则![]() 度
度
(2)拓展应用:如图5,在四边形ABCD中,![]() .O是四边形ABCD内一点,且
.O是四边形ABCD内一点,且![]() .求证:四边形OBCD是菱形.
.求证:四边形OBCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,各个角都相等,各条边都相等的多边形叫做正多边形.对一个各条边都相等的凸多边形(边数大于3),可以由若干条对角线相等判定它是正多边形.例如,各条边都相等的凸四边形,若两条对角线相等,则这个四边形是正方形.

(1)已知凸五边形![]() 的各条边都相等.
的各条边都相等.
①如图1,若![]() ,求证:五边形
,求证:五边形![]() 是正五边形;
是正五边形;
②如图2,若![]() ,请判断五边形
,请判断五边形![]() 是不是正五边形,并说明理由:
是不是正五边形,并说明理由:
(2)判断下列命题的真假.(在括号内填写“真”或“假”)
如图3,已知凸六边形![]() 的各条边都相等.
的各条边都相等.
①若![]() ,则六边形
,则六边形![]() 是正六边形;( )
是正六边形;( )
②若![]() ,则六边形
,则六边形![]() 是正六边形. ( )
是正六边形. ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顶点为![]() 的二次函数图象与x轴交于点
的二次函数图象与x轴交于点![]() ,点B在该图象上,
,点B在该图象上,![]() 交其对称轴l于点M,点M、N关于点P对称,连接
交其对称轴l于点M,点M、N关于点P对称,连接![]() 、
、![]() .
.
(1)求该二次函数的关系式.
(2)若点B在对称轴l右侧的二次函数图象上运动,请解答下列问题:
①连接![]() ,当
,当![]() 时,请判断
时,请判断![]() 的形状,并求出此时点B的坐标.
的形状,并求出此时点B的坐标.
②求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 经过点(2,3),对称轴为直线x =1.
经过点(2,3),对称轴为直线x =1.
(1)求抛物线的表达式;
(2)如果垂直于y轴的直线l与抛物线交于两点A(![]() ,
, ![]() ),B(
),B(![]() ,
, ![]() ),其中
),其中![]() ,
, ![]() ,与y轴交于点C,求BC
,与y轴交于点C,求BC![]() AC的值;
AC的值;
(3)将抛物线向上或向下平移,使新抛物线的顶点落在x轴上,原抛物线上一点P平移后对应点为点Q,如果OP=OQ,直接写出点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
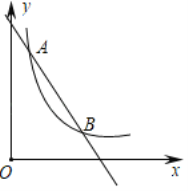
【题目】如图,一次函数![]() (k1、b为常数,k1≠0)的图象与反比例函数
(k1、b为常数,k1≠0)的图象与反比例函数![]()
![]() 的图象交于点A(m,8)与点B(4,2).
的图象交于点A(m,8)与点B(4,2).
①求一次函数与反比例函数的解析式.
②根据图象说明,当x为何值时,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个儿童游乐场所,由于周末小朋友较多,老板计划将场地扩建,扩建前平面图为△ABC,BC=10米,∠ABC=∠ACB=36°,扩建后顶点D在BA的延长线上,且∠BDC=90°,求扩建后AB边增加部分AD的长.(结果精确到0.1米.参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32,sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边由长为30米的篱笆围成.已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米.
(1)若苗圃园的面积为72平方米,求x;
(2)若平行于墙的一边长不小于8米,这个苗圃园的面积有最大值和最小值吗?如果有,求出最大值和最小值;如果没有,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
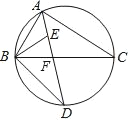
【题目】如图,∠BAC的平分线交AABC的外接圆于点D,交BC于点F,∠ABC的平分线交AD于点E.
(1)求证:DE=DB.
(2)若∠BAC=90°,BD=4,求△ABC外接圆的半径;
(3)若BD=6,DF=4,求AD的长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com