
【题目】阅读下列材料,解答问题:
为解方程![]() ,我们可以将
,我们可以将![]() 视为一个整体,然后设
视为一个整体,然后设![]() ,则
,则![]() ,原方程可化为
,原方程可化为![]() ,解此方程得
,解此方程得![]() .当
.当![]() 时,
时,![]() ,∴
,∴![]() ;当
;当![]() 时,
时,![]() ,∴
,∴![]() ,∴原方程的解为
,∴原方程的解为![]() .
.
(1)填空:在原方程得到方程(*)的过程中,利用________法达到了降次的目的,体现了________的数学思想;
(2)解方程:![]()
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的最大值为4,且该抛物线与
的最大值为4,且该抛物线与![]() 轴的交点为
轴的交点为![]() ,顶点为
,顶点为![]() .
.
(1)求该二次函数的解析式及点![]() ,
,![]() 的坐标;
的坐标;
(2)点![]() 是
是![]() 轴上的动点,
轴上的动点,
①求![]() 的最大值及对应的点
的最大值及对应的点![]() 的坐标;
的坐标;
②设![]() 是
是![]() 轴上的动点,若线段
轴上的动点,若线段![]() 与函数
与函数![]() 的图像只有一个公共点,求
的图像只有一个公共点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级全体男生1000米跑步的成绩,随机抽取了部分男生进行测试,并将测试成绩分为![]() 、
、![]() 、
、![]() 、
、![]() 四个等级,绘制如下不完整的统计图表,如题图表所示,根据图表信息解答下列问题:
四个等级,绘制如下不完整的统计图表,如题图表所示,根据图表信息解答下列问题:
成绩等级频数分布表
成绩等级 | 频数 |
A | 24 |
B | 10 |
C | x |
D | 2 |
合计 | y |
成绩等级扇形统计图

(1)x=______,y=______,扇形图中表示![]() 的圆心角的度数为______度;
的圆心角的度数为______度;
(2)甲、乙、丙是![]() 等级中的三名学生,学校决定从这三名学生中随机抽取两名介绍体育锻炼经验,用列表法或画树状图法,求同时抽到甲、乙两名学生的概率.
等级中的三名学生,学校决定从这三名学生中随机抽取两名介绍体育锻炼经验,用列表法或画树状图法,求同时抽到甲、乙两名学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,各个角都相等,各条边都相等的多边形叫做正多边形.对一个各条边都相等的凸多边形(边数大于3),可以由若干条对角线相等判定它是正多边形.例如,各条边都相等的凸四边形,若两条对角线相等,则这个四边形是正方形.

(1)已知凸五边形![]() 的各条边都相等.
的各条边都相等.
①如图1,若![]() ,求证:五边形
,求证:五边形![]() 是正五边形;
是正五边形;
②如图2,若![]() ,请判断五边形
,请判断五边形![]() 是不是正五边形,并说明理由:
是不是正五边形,并说明理由:
(2)判断下列命题的真假.(在括号内填写“真”或“假”)
如图3,已知凸六边形![]() 的各条边都相等.
的各条边都相等.
①若![]() ,则六边形
,则六边形![]() 是正六边形;( )
是正六边形;( )
②若![]() ,则六边形
,则六边形![]() 是正六边形. ( )
是正六边形. ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着粤港澳大湾区建设的加速推进,广东省正加速布局以5G等为代表的战略性新兴产业,据统计,目前广东5G基站的数量约1.5万座,计划到2020年底,全省5G基站数是目前的4倍,到2022年底,全省5G基站数量将达到17.34万座。
(1)计划到2020年底,全省5G基站的数量是多少万座?;
(2)按照计划,求2020年底到2022年底,全省5G基站数量的年平均增长率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顶点为![]() 的二次函数图象与x轴交于点
的二次函数图象与x轴交于点![]() ,点B在该图象上,
,点B在该图象上,![]() 交其对称轴l于点M,点M、N关于点P对称,连接
交其对称轴l于点M,点M、N关于点P对称,连接![]() 、
、![]() .
.
(1)求该二次函数的关系式.
(2)若点B在对称轴l右侧的二次函数图象上运动,请解答下列问题:
①连接![]() ,当
,当![]() 时,请判断
时,请判断![]() 的形状,并求出此时点B的坐标.
的形状,并求出此时点B的坐标.
②求证:![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
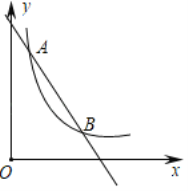
【题目】如图,一次函数![]() (k1、b为常数,k1≠0)的图象与反比例函数
(k1、b为常数,k1≠0)的图象与反比例函数![]()
![]() 的图象交于点A(m,8)与点B(4,2).
的图象交于点A(m,8)与点B(4,2).
①求一次函数与反比例函数的解析式.
②根据图象说明,当x为何值时,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
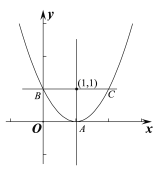
【题目】已知抛物y=ax2+bx+c(b<0)与轴只有一个公共点.
(1)若公共点坐标为(2,0),求a、c满足的关系式;
(2)设A为抛物线上的一定点,直线l:y=kx+1-k与抛物线交于点B、C两点,直线BD垂直于直线y=-1,垂足为点D.当k=0时,直线l与抛物线的一个交点在y轴上,且△ABC为等腰直角三角形.
①求点A的坐标和抛物线的解析式;
②证明:对于每个给定的实数k,都有A、D、C三点共线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com