
ΓΨΧβΡΩΓΩ“―÷Σ≈ΉΈοy=ax2+bx+c(b<0)”κ÷α÷Μ”–“ΜΗωΙΪΙ≤Βψ.
(1)»τΙΪΙ≤ΒψΉχ±ξΈΣ(2Θ§0)Θ§«σaΓΔc¬ζΉψΒΡΙΊœΒ ΫΘΜ
(2)…ηAΈΣ≈ΉΈοœΏ…œΒΡ“ΜΕ®ΒψΘ§÷±œΏlΘΚy=kx+1Θ≠k”κ≈ΉΈοœΏΫΜ”ΎΒψBΓΔCΝΫΒψΘ§÷±œΏBD¥Ι÷±”Ύ÷±œΏy=Θ≠1,¥ΙΉψΈΣΒψD.Β±kΘΫ0 ±Θ§÷±œΏl”κ≈ΉΈοœΏΒΡ“ΜΗωΫΜΒψ‘Ύy÷α…œΘ§«“ΓςABCΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–Έ.
ΔΌ«σΒψAΒΡΉχ±ξΚΆ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
ΔΎ÷ΛΟςΘΚΕ‘”ΎΟΩΗωΗχΕ®ΒΡ Β ΐkΘ§ΕΦ”–AΓΔDΓΔC»ΐΒψΙ≤œΏ.
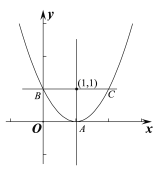
ΓΨ¥πΑΗΓΩ(1) y=a(xΘ≠2)2, c=4a;(2) ΔΌΕΞΒψA(1,0)Θ§y= x2Θ≠2x+1,ΔΎΦϊΫβΈω.
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨί≈ΉΈοœΏ”κx÷αΒΡΙΪΙ≤ΒψΉχ±ξΦ¥ΈΣΚ· ΐΕΞΒψΉχ±ξΘ§Φ¥Ω…«σΫβΘΜ
Θ®2Θ©ΔΌyΘΫkxΘΪ1kΘΫkΘ®x1Θ©ΘΪ1ΙΐΕ®ΒψΘ®1Θ§1Θ©Θ§«“Β±kΘΫ0 ±Θ§÷±œΏl±δΈΣyΘΫ1ΤΫ––x÷αΘ§”κ÷αΒΡΫΜΒψΈΣΘ®0Θ§1Θ©Θ§Φ¥Ω…«σΫβΘΜΔΎΦΤΥψ÷±œΏAD±μ¥ο Ϋ÷–ΒΡk÷ΒΓΔ÷±œΏAC±μ¥ο Ϋ÷–ΒΡk÷ΒΘ§ΝΫΗωk÷ΒœύΒ»Φ¥Ω…«σΫβΘ°
ΫβΘΚΘ®1Θ©≈ΉΈοœΏ”κx÷αΒΡΙΪΙ≤ΒψΉχ±ξΦ¥ΈΣΚ· ΐΕΞΒψΉχ±ξΘ§Ι ΘΚyΘΫaΘ®x2Θ©2Θ§‘ρcΘΫ4aΘΜ
(2) y=kx+1Θ≠k= k(xΘ≠1)+1ΙΐΕ®Βψ(1,1),
«“Β±kΘΫ0 ±Θ§÷±œΏl±δΈΣy=1ΤΫ––x÷α,”κy÷αΒΡΫΜΒψΈΣ(0,1)
”÷ΓςABCΈΣΒ»―ϋ÷±Ϋ«»ΐΫ«–ΈΘ§ΓύΒψAΈΣ≈ΉΈοœΏΒΡΕΞΒψ
ΔΌc=1Θ§ΕΞΒψA(1,0)
≈ΉΈοœΏΒΡΫβΈω Ϋ: y= x2Θ≠2x+1.
ΔΎ![]()
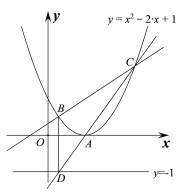
x2Θ≠(2+k)x+kΘΫ0,
xΘΫ![]() (2+kΓά
(2+kΓά![]() )
)
xDΘΫxBΘΫ![]() (2+kΘ≠
(2+kΘ≠![]() ), yD=Θ≠1ΘΜ
), yD=Θ≠1ΘΜ
‘ρD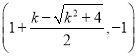
yCΘΫ![]() (2+k2+k
(2+k2+k![]() ,
,
C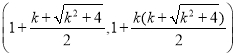 Θ§A(1,0)
Θ§A(1,0)
Γύ÷±œΏAD±μ¥ο Ϋ÷–ΒΡk÷ΒΈΣΘΚk AD=![]() =
=![]() Θ§
Θ§
÷±œΏAC±μ¥ο Ϋ÷–ΒΡk÷ΒΈΣΘΚk AC=![]()
Γύk AD= k AC, ΒψAΓΔCΓΔD»ΐΒψΙ≤œΏ.


 ”Π”ΟΧβΉς“Β±ΨœΒΝ–¥πΑΗ
”Π”ΟΧβΉς“Β±ΨœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΡΕΝœ¬Ν–≤ΡΝœΘ§Ϋβ¥πΈ ΧβΘΚ
ΈΣΫβΖΫ≥Χ![]() Θ§Έ“Ο«Ω…“‘ΫΪ
Θ§Έ“Ο«Ω…“‘ΫΪ![]() ”ΈΣ“ΜΗω’ϊΧεΘ§»ΜΚσ…η
”ΈΣ“ΜΗω’ϊΧεΘ§»ΜΚσ…η![]() Θ§‘ρ
Θ§‘ρ![]() Θ§‘≠ΖΫ≥ΧΩ…Μ·ΈΣ
Θ§‘≠ΖΫ≥ΧΩ…Μ·ΈΣ![]() Θ§Ϋβ¥ΥΖΫ≥ΧΒΟ
Θ§Ϋβ¥ΥΖΫ≥ΧΒΟ![]() .Β±
.Β±![]() ±Θ§
±Θ§![]() Θ§Γύ
Θ§Γύ![]() ΘΜΒ±
ΘΜΒ±![]() ±Θ§
±Θ§![]() Θ§Γύ
Θ§Γύ![]() Θ§Γύ‘≠ΖΫ≥ΧΒΡΫβΈΣ
Θ§Γύ‘≠ΖΫ≥ΧΒΡΫβΈΣ![]() .
.
(1)ΧνΩ’ΘΚ‘Ύ‘≠ΖΫ≥ΧΒΟΒΫΖΫ≥Χ(*)ΒΡΙΐ≥Χ÷–Θ§άϊ”Ο________Ζ®¥οΒΫΝΥΫΒ¥ΈΒΡΡΩΒΡΘ§Χεœ÷ΝΥ________ΒΡ ΐ―ßΥΦœκΘΜ
(2)ΫβΖΫ≥ΧΘΚ![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣAB=ADΘ§Ρ«Ο¥ΧμΦ”œ¬Ν–“ΜΗωΧθΦΰΚσΘ§»‘ΈόΖ®≈–Ε®ΓςABCΓ’ΓςADCΒΡ «Θ®ΓΓΓΓΘ©

A. CB=CD B. ΓœBAC=ΓœDAC C. ΓœBCA=ΓœDCA D. ΓœB=ΓœD=90Γψ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§»τ“Σ‘ΎΩμADΈΣ20ΟΉΒΡ≥«Ρœ¥σΒάΝΫ±ΏΑ≤ΉΑ¬ΖΒΤΘ§¬ΖΒΤΒΡΒΤ±έBC≥Λ2ΟΉΘ§«“”κΒΤ÷υAB≥…120ΓψΫ«Θ§¬ΖΒΤ≤…”Ο‘≤ΉΕ–ΈΒΤ’÷Θ§ΒΤ’÷ΒΡ÷αœΏCO”κΒΤ±έBC¥Ι÷±Θ§Β±ΒΤ’÷ΒΡ÷αœΏCOΆ®ΙΐΙΪ¬Ζ¬ΖΟφΒΡ÷––ΡœΏ ±’’Ος–ßΙϊΉνΚΟΘ§¥Υ ±Θ§¬ΖΒΤΒΡΒΤ÷υABΗΏ”ΠΗΟ…ηΦΤΈΣΕύ…ΌΟΉΘ®ΫαΙϊ±ΘΝτΗυΚ≈Θ©ΘΩ

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷ΣΓςABCΈΣΚΆΒψA'.
(1)“‘ΒψA'ΈΣΕΞΒψ«σΉςΓςA'B'C', ΙΓςA'B'C'ΓΉΓςABCΘ§SΓςA'B'C'=4SΓςABC;
(≥ΏΙφΉςΆΦΘ§±ΘΝτΉςΆΦΚέΦΘΘ§≤Μ–¥ΉςΖ®)
(2)…ηDΓΔEΓΔFΖ÷±π «ΓςABC»ΐ±ΏABΓΔBCΓΔACΒΡ÷–ΒψΘ§D'ΓΔE'ΓΔF'Ζ÷±π «ΡψΥυΉςΒΡΓςA'B'C'»ΐ±ΏA'B'ΓΔB'C'ΓΔA'C'ΒΡ÷–ΒψΘ§«σ÷ΛΘΚΓςDEFΓΉΓςD'E'F'.

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘Ύ![]() ÷–Θ§
÷–Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() ”ΎΒψ
”ΎΒψ![]() Θ°
Θ°
Θ®1Θ©»γΆΦ1Θ§Βψ![]() Θ§
Θ§![]() Ζ÷±π‘Ύ
Ζ÷±π‘Ύ![]() Θ§
Θ§![]() …œΘ§«“
…œΘ§«“![]() Θ§Β±
Θ§Β±![]() Θ§
Θ§![]() ±Θ§«σœΏΕΈ
±Θ§«σœΏΕΈ![]() ΒΡ≥ΛΘΜ
ΒΡ≥ΛΘΜ
Θ®2Θ©»γΆΦ2Θ§Βψ![]() Θ§
Θ§![]() Ζ÷±π‘Ύ
Ζ÷±π‘Ύ![]() Θ§
Θ§![]() …œΘ§«“
…œΘ§«“![]() Θ§«σ÷ΛΘΚ
Θ§«σ÷ΛΘΚ![]() ΘΜ
ΘΜ
Θ®3Θ©»γΆΦ3Θ§Βψ![]() ‘Ύ
‘Ύ![]() ΒΡ―”≥ΛœΏ…œΘ§Βψ
ΒΡ―”≥ΛœΏ…œΘ§Βψ![]() ‘Ύ
‘Ύ![]() …œΘ§«“
…œΘ§«“![]() Θ§«σ÷ΛΘΚ
Θ§«σ÷ΛΘΚ![]() Θ°
Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΓΕ»γΙϊœκΜΌΒτ“ΜΗωΚΔΉ”Θ§ΨΆΗχΥϊ“Μ≤Ω ÷Μζ!ΓΖ’β «2017ΡξΈΔ–≈»Π“ΜΤΣ»»¥ΪΒΡΈΡ’¬Θ°ΙζΦ …œΘ§Ζ®ΙζΫΧ”ΐ≤Ω–ϊ≤Φ¥” 2018 Ρξ9‘¬–¬―ßΤΎΤπ–Γ―ßΚΆ≥θ÷–Ϋϊ÷Ι―ß…ζ Ι”Ο ÷ΜζΘ°ΈΣΝΥΫβ―ß…ζ ÷Μζ Ι”Ο«ιΩωΘ§Ρ≥―ß–ΘΩΣ’ΙΝΥΓΑ ÷ΜζΑιΈ“ΫΓΩΒ––Γ±÷ςΧβΜνΕ·Θ§ΥϊΟ«ΥφΜζ≥ι»Γ≤ΩΖ÷―ß…ζΫχ––ΓΑ Ι”Ο ÷ΜζΡΩΒΡΓ±ΚΆΓΑΟΩ÷ή Ι”Ο ÷ΜζΒΡ ±ΦδΓ±ΒΡΈ ΨμΒς≤ιΘ§≤ΔΜφ÷Τ≥…»γΆΦΔΌΘ§ΔΎΒΡ Ά≥ΦΤΆΦΘ§“―÷ΣΓΑ≤ιΉ ΝœΓ±ΒΡ»Υ ΐ « 40»ΥΘ°«κΡψΗυΨί“‘…œ–≈œΔΫβ¥πœ¬Ν–Έ ΧβΘΚ
(1)‘Ύ…»–ΈΆ≥ΦΤΆΦ÷–Θ§ΓΑΆφ”ΈœΖΓ±Ε‘”ΠΒΡΑΌΖ÷±»ΈΣ______Θ§‘≤–ΡΫ«Ε» ΐ «______Ε»ΘΜ
(2)≤Ι»ΪΧθ–ΈΆ≥ΦΤΆΦΘΜ
(3)ΗΟ–ΘΙ≤”–―ß…ζ2100»ΥΘ§ΙάΦΤΟΩ÷ή Ι”Ο ÷Μζ ±Φδ‘Ύ2 –Γ ±“‘…œ(≤ΜΚ§2–Γ ±)ΒΡ»Υ ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ![]() ÷–Θ§“―÷Σ≈ΉΈοœΏ
÷–Θ§“―÷Σ≈ΉΈοœΏ![]() ”κ÷±œΏ
”κ÷±œΏ![]() ΕΦΨ≠Ιΐ
ΕΦΨ≠Ιΐ![]() ΓΔ
ΓΔ![]() ΝΫΒψΘ§ΗΟ≈ΉΈοœΏΒΡΕΞΒψΈΣCΘ°
ΝΫΒψΘ§ΗΟ≈ΉΈοœΏΒΡΕΞΒψΈΣCΘ°
Θ®1Θ©«σ¥Υ≈ΉΈοœΏΚΆ÷±œΏ![]() ΒΡΫβΈω ΫΘΜ
ΒΡΫβΈω ΫΘΜ
Θ®2Θ©…η÷±œΏ![]() ”κΗΟ≈ΉΈοœΏΒΡΕ‘≥Τ÷αΫΜ”ΎΒψEΘ§‘Ύ…δœΏ
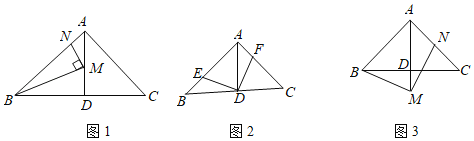
”κΗΟ≈ΉΈοœΏΒΡΕ‘≥Τ÷αΫΜ”ΎΒψEΘ§‘Ύ…δœΏ![]() …œ «Ζώ¥φ‘Ύ“ΜΒψMΘ§ΙΐMΉςx÷αΒΡ¥ΙœΏΫΜ≈ΉΈοœΏ”ΎΒψNΘ§ ΙΒψMΓΔNΓΔCΓΔE «ΤΫ––ΥΡ±Ώ–ΈΒΡΥΡΗωΕΞΒψΘΩ»τ¥φ‘ΎΘ§«σΒψMΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…ΘΜ
…œ «Ζώ¥φ‘Ύ“ΜΒψMΘ§ΙΐMΉςx÷αΒΡ¥ΙœΏΫΜ≈ΉΈοœΏ”ΎΒψNΘ§ ΙΒψMΓΔNΓΔCΓΔE «ΤΫ––ΥΡ±Ώ–ΈΒΡΥΡΗωΕΞΒψΘΩ»τ¥φ‘ΎΘ§«σΒψMΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…ΘΜ
Θ®3Θ©…ηΒψP «÷±œΏ![]() œ¬ΖΫ≈ΉΈοœΏ…œΒΡ“ΜΕ·ΒψΘ§Β±
œ¬ΖΫ≈ΉΈοœΏ…œΒΡ“ΜΕ·ΒψΘ§Β±![]() ΟφΜΐΉν¥σ ±Θ§«σΒψPΒΡΉχ±ξΘ§≤Δ«σ
ΟφΜΐΉν¥σ ±Θ§«σΒψPΒΡΉχ±ξΘ§≤Δ«σ![]() ΟφΜΐΒΡΉν¥σ÷ΒΘ°
ΟφΜΐΒΡΉν¥σ÷ΒΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ≈ΉΈοœΏ![]() Ψ≠ΙΐΒψ
Ψ≠ΙΐΒψ![]() Θ§”κ
Θ§”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() Θ°
Θ°
![]() «σ’βΧθ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
«σ’βΧθ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
![]() »γΆΦ1Θ§ΒψP «ΒΎ»ΐœσœόΡΎ≈ΉΈοœΏ…œΒΡ“ΜΗωΕ·ΒψΘ§Β±ΥΡ±Ώ–Έ
»γΆΦ1Θ§ΒψP «ΒΎ»ΐœσœόΡΎ≈ΉΈοœΏ…œΒΡ“ΜΗωΕ·ΒψΘ§Β±ΥΡ±Ώ–Έ![]() ΒΡΟφΜΐΉν¥σ ±Θ§«σΒψ
ΒΡΟφΜΐΉν¥σ ±Θ§«σΒψ![]() ΒΡΉχ±ξΘΜ
ΒΡΉχ±ξΘΜ
![]() »γΆΦ2Θ§œΏΕΈ
»γΆΦ2Θ§œΏΕΈ![]() ΒΡ¥Ι÷±ΤΫΖ÷œΏΫΜ
ΒΡ¥Ι÷±ΤΫΖ÷œΏΫΜ![]() ÷α”ΎΒψ
÷α”ΎΒψ![]() Θ§¥ΙΉψΈΣ
Θ§¥ΙΉψΈΣ![]() ΈΣ≈ΉΈοœΏΒΡΕΞΒψΘ§‘Ύ÷±œΏ
ΈΣ≈ΉΈοœΏΒΡΕΞΒψΘ§‘Ύ÷±œΏ![]() …œ «Ζώ¥φ‘Ύ“ΜΒψ
…œ «Ζώ¥φ‘Ύ“ΜΒψ![]() Θ§ Ι
Θ§ Ι![]() ΒΡ÷ή≥ΛΉν–ΓΘΩ»τ¥φ‘ΎΘ§«σ≥ωΒψ
ΒΡ÷ή≥ΛΉν–ΓΘΩ»τ¥φ‘ΎΘ§«σ≥ωΒψ![]() ΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com