
【题目】如图,![]() 中,
中,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,
上,![]() ,
,![]() .点
.点![]() 是线段
是线段![]() 上一动点,当半径为6的圆
上一动点,当半径为6的圆![]() 与
与![]() 的一边相切时,
的一边相切时,![]() 的长为________.
的长为________.

【答案】![]() 或
或![]()
【解析】
根据勾股定理得到![]() ,
,![]() ,当⊙P于BC相切时,点P到BC的距离=6,过P作PH⊥BC于H,则PH=6,当⊙P于AB相切时,点P到AB的距离=6,根据相似三角形的性质即可得到结论.
,当⊙P于BC相切时,点P到BC的距离=6,过P作PH⊥BC于H,则PH=6,当⊙P于AB相切时,点P到AB的距离=6,根据相似三角形的性质即可得到结论.
∵在Rt△ABC中,∠C=90°,AC=12,BD+CD=18,
∴![]() ,
,
在Rt△ADC中,∠C=90°,AC=12,CD=5,
∴![]() ,
,
当⊙P于BC相切时,点P到BC的距离=6,
过P作PH⊥BC于H,则PH=6,
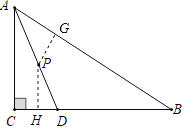
∵∠C=90°,
∴AC⊥BC,
∴PH∥AC,
∴△DPH∽△DAC,
∴![]() ,
,
∴![]() ,
,
∴PD=6.5,
∴AP=6.5;
当⊙P于AB相切时,点P到AB的距离=6,
过P作PG⊥AB于G,
则PG=6,
∵AD=BD=13,
∴∠PAG=∠B,
∵∠AGP=∠C=90°,
∴△AGP∽△BCA,
∴![]() ,
,
∴![]() ,
,
∴AP=3![]() ,
,
∵CD=5<6,
∴半径为6的⊙P不与△ABC的AC边相切,
综上所述,AP的长为6.5或3![]() ,
,
故答案为:6.5或3![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
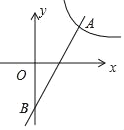
【题目】如图在平面直角坐标系xOy中,一次函数y=2x﹣2的图象与函数y=![]() (k≠0)的图象有交点为A(m,2),与y轴交于点B
(k≠0)的图象有交点为A(m,2),与y轴交于点B
(1)求反比例函数的解析式;
(2)若函数y=![]() 在第一象限的图象上有一点P,且△POB的面积为6,求点P坐标.
在第一象限的图象上有一点P,且△POB的面积为6,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
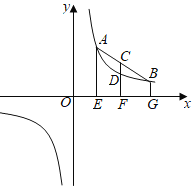
【题目】(1)阅读理解
如图,点![]() ,
,![]() 在反比例函数
在反比例函数![]() 的图象上,连接
的图象上,连接![]() ,取线段
,取线段![]() 的中点
的中点![]() .分别过点
.分别过点![]() ,
,![]() ,
,![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,
,![]() ,
,![]() ,
,![]() 交反比例函数
交反比例函数![]() 的图象于点
的图象于点![]() .点
.点![]() ,
,![]() ,
,![]() 的横坐标分别为
的横坐标分别为![]() ,
,![]() ,
,![]() .小红通过观察反比例函数
.小红通过观察反比例函数![]() 的图象,并运用几何知识得出结论:AE+BG=2CF,CF>DF,由此得出一个关于
的图象,并运用几何知识得出结论:AE+BG=2CF,CF>DF,由此得出一个关于![]() ,
,![]() ,
,![]() 之间数量关系的命题:若
之间数量关系的命题:若![]() ,则______.
,则______.
(2)证明命题
小东认为:可以通过“若![]() ,则
,则![]() ”的思路证明上述命题.
”的思路证明上述命题.
小晴认为:可以通过“若![]() ,
,![]() ,且
,且![]() ,则
,则![]() ”的思路证明上述命题.
”的思路证明上述命题.
请你选择一种方法证明(1)中的命题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:有两个相邻内角互余的四边形称为邻余四边形,这两个角的夹边称为邻余线.
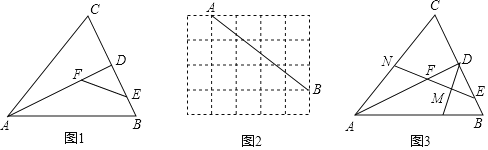
(1)如图1,在![]() 中,
中,![]() ,
,![]() 是
是![]() 的角平分线,
的角平分线,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 上的点.求证:四边形
上的点.求证:四边形![]() 是邻余四边形.
是邻余四边形.
(2)如图2,在![]() 的方格纸中,
的方格纸中,![]() ,
,![]() 在格点上,请画出一个符合条件的邻余四边形
在格点上,请画出一个符合条件的邻余四边形![]() ,使
,使![]() 是邻余线,
是邻余线,![]() ,
,![]() 在格点上.
在格点上.
(3)如图3,在(1)的条件下,取![]() 中点
中点![]() ,连结
,连结![]() 并延长交
并延长交![]() 于点
于点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() .若
.若![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() ,求邻余线
,求邻余线![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
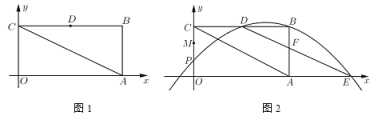
【题目】如图1,已知在平面直角坐标系![]() 中,四边形
中,四边形![]() 是矩形点
是矩形点![]() 分别在
分别在![]() 轴和
轴和![]() 轴的正半轴上,连结
轴的正半轴上,连结![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.
(1)求OC的长和点![]() 的坐标;
的坐标;
(2)如图2,![]() 是线段
是线段![]() 上的点,
上的点,![]() ,点
,点![]() 是线段
是线段![]() 上的一个动点,经过
上的一个动点,经过![]() 三点的抛物线交
三点的抛物线交![]() 轴的正半轴于点
轴的正半轴于点![]() ,连结
,连结![]() 交
交![]() 于点
于点![]()
①将![]() 沿
沿![]() 所在的直线翻折,若点
所在的直线翻折,若点![]() 恰好落在
恰好落在![]() 上,求此时
上,求此时![]() 的长和点
的长和点![]() 的坐标;
的坐标;
②以线段![]() 为边,在
为边,在![]() 所在直线的右上方作等边
所在直线的右上方作等边![]() ,当动点
,当动点![]() 从点
从点![]() 运动到点
运动到点![]() 时,点
时,点![]() 也随之运动,请直接写出点
也随之运动,请直接写出点![]() 运动路径的长.
运动路径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是某酒店的推拉门,已知门的宽度AD=2米,两扇门的大小相同(即AB=CD),且AB+CD=AD,现将右边的门CDD1C1绕门轴DD1向外面旋转67°(如图2所示).
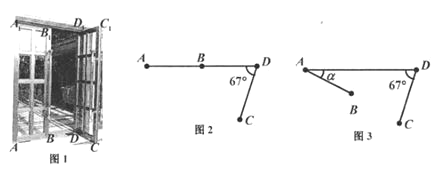
参考数据:(sin67°≈0.92,cos67°≈0.39,tan29.6°≈0.57,tan19.6°≈0.36,sin29.6°≈0.49)
(1)求点C到直线AD的距离.
(2)将左边的门ABB1A1绕门轴AA1向外面旋转,设旋转角为a(如图3所示),问当a为多少度时,点B,C之间的距离最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
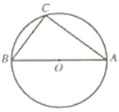
【题目】如图,⊙O的直径AB=10,弦AC=8,连接BC。
(1)尺规作图:作弦CD,使CD=BC(点D不与B重合),连接AD;(保留作图痕迹,不写作法)
(2)在(1)所作的图中,求四边形ABCD的周长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com