
【题目】图1是某酒店的推拉门,已知门的宽度AD=2米,两扇门的大小相同(即AB=CD),且AB+CD=AD,现将右边的门CDD1C1绕门轴DD1向外面旋转67°(如图2所示).
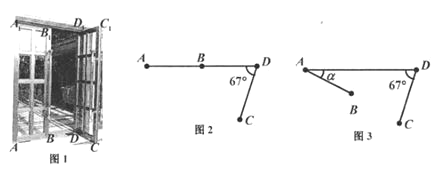
参考数据:(sin67°≈0.92,cos67°≈0.39,tan29.6°≈0.57,tan19.6°≈0.36,sin29.6°≈0.49)
(1)求点C到直线AD的距离.
(2)将左边的门ABB1A1绕门轴AA1向外面旋转,设旋转角为a(如图3所示),问当a为多少度时,点B,C之间的距离最短.
【答案】(1)点C到直线AD的距离为0.92米;(2)当旋转角为a为29.6°时,点B,C之间的距离最短.
【解析】
利用三角函数的应用(1)作CE⊥AD交AD于点E,根据![]() ,求出CE的值,即C点到AD的距离.(2)要使点B,C之间的距离最短,只需满足AB所在的直线经过点C.由(1)可知CE的长利用cos67°求出DE的长,然后算出AE,根据tanA=
,求出CE的值,即C点到AD的距离.(2)要使点B,C之间的距离最短,只需满足AB所在的直线经过点C.由(1)可知CE的长利用cos67°求出DE的长,然后算出AE,根据tanA= ![]() ,求出∠A的度数.
,求出∠A的度数.
(1)解: 作CE⊥AD交AD于点E.

∴sin 67°= ![]()
即CE=CD sin 67°=1×0.92=0.92.
∴点C到直线AD的距离为0.92米.
(2)解:要使点B,C之间的距离最短,只需满足AB所在的直线经过点C.(如图3)

由(1)知CE=0.92,DE=CD cos67°=1×0.39=0.39.
∴AE=2-0.39=1.61.
∴在Rt△AEC中,tanA= ![]() =
=![]() ≈0.57.
≈0.57.
∴∠A=29.6°.
即当旋转角为a为29.6°时,点B,C之间的距离最短.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() .
.

(1)如图①,点![]() 在斜边
在斜边![]() 上,以点
上,以点![]() 为圆心,
为圆心,![]() 长为半径的圆交
长为半径的圆交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,与边
,与边![]() 相切于点
相切于点![]() .求证:
.求证:![]() ;
;
(2)在图②中作![]() ,使它满足以下条件:
,使它满足以下条件:
①圆心在边![]() 上;②经过点
上;②经过点![]() ;③与边
;③与边![]() 相切.
相切.
(尺规作图,只保留作图痕迹,不要求写出作法)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】箭头四角形,模型规律:如图1,延长CO交AB于点D,则![]() .因为凹四边形ABOC形似箭头,其四角具有“
.因为凹四边形ABOC形似箭头,其四角具有“![]() ”这个规律,所以我们把这个模型叫做“箭头四角形”.模型应用:
”这个规律,所以我们把这个模型叫做“箭头四角形”.模型应用:
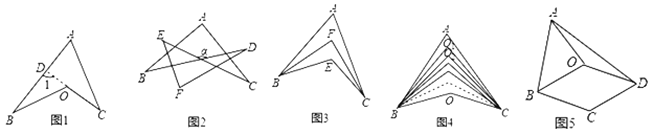
(1)直接应用:
①如图2,![]() .
.
②如图3,![]() 的2等分线(即角平分线)
的2等分线(即角平分线)![]() 交于点F,已知
交于点F,已知![]() ,则
,则![]()
③如图4,![]() 分别为
分别为![]() 的2019等分线
的2019等分线![]() .它们的交点从上到下依次为
.它们的交点从上到下依次为![]() .已知
.已知![]() ,则
,则![]() 度
度
(2)拓展应用:如图5,在四边形ABCD中,![]() .O是四边形ABCD内一点,且
.O是四边形ABCD内一点,且![]() .求证:四边形OBCD是菱形.
.求证:四边形OBCD是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在扇形OAB中,点C是弧AB上任意一点(不与点A,B重合),CD∥OA交OB于点D,点I是△OCD的内心,连结OI,BI.若∠AOB=β,则∠OIB等于( )

A. 180°![]() βB. 180°-βC. 90°+
βB. 180°-βC. 90°+ ![]() βD. 90°+β
βD. 90°+β
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级全体男生1000米跑步的成绩,随机抽取了部分男生进行测试,并将测试成绩分为![]() 、
、![]() 、
、![]() 、
、![]() 四个等级,绘制如下不完整的统计图表,如题图表所示,根据图表信息解答下列问题:
四个等级,绘制如下不完整的统计图表,如题图表所示,根据图表信息解答下列问题:
成绩等级频数分布表
成绩等级 | 频数 |
A | 24 |
B | 10 |
C | x |
D | 2 |
合计 | y |
成绩等级扇形统计图

(1)x=______,y=______,扇形图中表示![]() 的圆心角的度数为______度;
的圆心角的度数为______度;
(2)甲、乙、丙是![]() 等级中的三名学生,学校决定从这三名学生中随机抽取两名介绍体育锻炼经验,用列表法或画树状图法,求同时抽到甲、乙两名学生的概率.
等级中的三名学生,学校决定从这三名学生中随机抽取两名介绍体育锻炼经验,用列表法或画树状图法,求同时抽到甲、乙两名学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
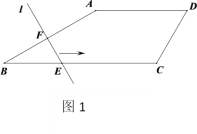
【题目】如图1,在四边形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,直线
,直线![]() .当直线
.当直线![]() 沿射线
沿射线![]() 方向,从点
方向,从点![]() 开始向右平移时,直线
开始向右平移时,直线![]() 与四边形
与四边形![]() 的边分别相交于点
的边分别相交于点![]() 、
、![]() .设直线
.设直线![]() 向右平移的距离为
向右平移的距离为![]() ,线段
,线段![]() 的长为
的长为![]() ,且
,且![]() 与
与![]() 的函数关系如图2所示,则四边形
的函数关系如图2所示,则四边形![]() 的周长是_____.
的周长是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,各个角都相等,各条边都相等的多边形叫做正多边形.对一个各条边都相等的凸多边形(边数大于3),可以由若干条对角线相等判定它是正多边形.例如,各条边都相等的凸四边形,若两条对角线相等,则这个四边形是正方形.

(1)已知凸五边形![]() 的各条边都相等.
的各条边都相等.
①如图1,若![]() ,求证:五边形
,求证:五边形![]() 是正五边形;
是正五边形;
②如图2,若![]() ,请判断五边形
,请判断五边形![]() 是不是正五边形,并说明理由:
是不是正五边形,并说明理由:
(2)判断下列命题的真假.(在括号内填写“真”或“假”)
如图3,已知凸六边形![]() 的各条边都相等.
的各条边都相等.
①若![]() ,则六边形
,则六边形![]() 是正六边形;( )
是正六边形;( )
②若![]() ,则六边形
,则六边形![]() 是正六边形. ( )
是正六边形. ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个儿童游乐场所,由于周末小朋友较多,老板计划将场地扩建,扩建前平面图为△ABC,BC=10米,∠ABC=∠ACB=36°,扩建后顶点D在BA的延长线上,且∠BDC=90°,求扩建后AB边增加部分AD的长.(结果精确到0.1米.参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.32,sin36°≈0.59,cos36°≈0.81,tan36°≈0.73)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com