
【题目】如图,在扇形OAB中,点C是弧AB上任意一点(不与点A,B重合),CD∥OA交OB于点D,点I是△OCD的内心,连结OI,BI.若∠AOB=β,则∠OIB等于( )

A. 180°![]() βB. 180°-βC. 90°+
βB. 180°-βC. 90°+ ![]() βD. 90°+β
βD. 90°+β
【答案】A
【解析】
首先根据平行线的性质得出∠AOC=∠OCD,根据角的和差及等量代换得出∠OCD+∠COB= β ,然后根据三角形内心的定义得出∠COI+∠OCI=![]() , 进而根据三角形的内角和得出∠OIC=180°-
, 进而根据三角形的内角和得出∠OIC=180°- ![]() β,最后根据SAS判断出△COI≌△BOI,根据全等三角形对应角相等得出∠OIB =∠OIC,从而得出答案
β,最后根据SAS判断出△COI≌△BOI,根据全等三角形对应角相等得出∠OIB =∠OIC,从而得出答案
连接IC,
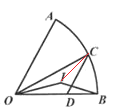
∵ CD∥OA ,
∴∠AOC=∠OCD,
∵∠AOC+∠COB=∠AOB= β ,
∴∠OCD+∠COB= β ,
∵ 点I是△OCD的内心 ,
∴∠COI+∠OCI=![]() ,
,
∴ ∠OIC=180°-(∠COI+∠OCI)= 180°- ![]() β ;
β ;
在△COI与△BOI中,
∵OC=OB,∠COI=∠BOI,OI=OI,
∴△COI≌△BOI,
∴ ∠OIB =∠OIC= 180°- ![]() β.
β.
故答案为:A.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
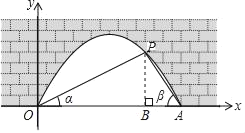
【题目】如图是抛物线形拱桥,P处有一照明灯,水面OA宽4m,从O、A两处双测P处,仰角分别为α、β,且tanα=![]() ,tanβ=
,tanβ=![]() ,以O为原点,OA所在直线为x轴建立直角坐标系. P点坐标为_____;若水面上升1m,水面宽为_____m.
,以O为原点,OA所在直线为x轴建立直角坐标系. P点坐标为_____;若水面上升1m,水面宽为_____m.
查看答案和解析>>
科目:初中数学 来源: 题型:
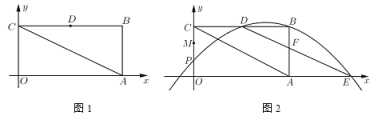
【题目】如图1,已知在平面直角坐标系![]() 中,四边形
中,四边形![]() 是矩形点
是矩形点![]() 分别在
分别在![]() 轴和
轴和![]() 轴的正半轴上,连结
轴的正半轴上,连结![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 的中点.
的中点.
(1)求OC的长和点![]() 的坐标;
的坐标;
(2)如图2,![]() 是线段
是线段![]() 上的点,
上的点,![]() ,点
,点![]() 是线段
是线段![]() 上的一个动点,经过
上的一个动点,经过![]() 三点的抛物线交
三点的抛物线交![]() 轴的正半轴于点
轴的正半轴于点![]() ,连结
,连结![]() 交
交![]() 于点
于点![]()
①将![]() 沿
沿![]() 所在的直线翻折,若点
所在的直线翻折,若点![]() 恰好落在
恰好落在![]() 上,求此时
上,求此时![]() 的长和点
的长和点![]() 的坐标;
的坐标;
②以线段![]() 为边,在
为边,在![]() 所在直线的右上方作等边
所在直线的右上方作等边![]() ,当动点
,当动点![]() 从点
从点![]() 运动到点
运动到点![]() 时,点
时,点![]() 也随之运动,请直接写出点
也随之运动,请直接写出点![]() 运动路径的长.
运动路径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据有理数乘法(除法)法则可知:①若![]() (或
(或![]() ),则
),则![]() 或
或![]() ;②若
;②若![]() (或
(或![]() ),则
),则![]() 或
或![]() .
.
根据上述知识,求不等式![]() 的解集:
的解集:
解:原不等式可化为:(1)![]() 或(2)
或(2)![]() .
.
由(1)得,![]() ,由(2)得,
,由(2)得,![]() ,
,
∴原不等式的解集为:![]() 或
或![]()
请你运用所学知识,结合上述材料解答下列问题:
(1)不等式![]() 的解集为 .
的解集为 .
(2)求不等式![]() 的解集(要求写出解答过程)
的解集(要求写出解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是某酒店的推拉门,已知门的宽度AD=2米,两扇门的大小相同(即AB=CD),且AB+CD=AD,现将右边的门CDD1C1绕门轴DD1向外面旋转67°(如图2所示).
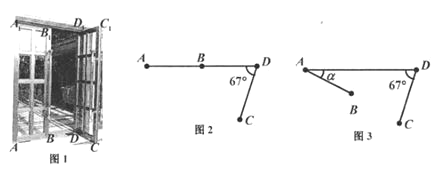
参考数据:(sin67°≈0.92,cos67°≈0.39,tan29.6°≈0.57,tan19.6°≈0.36,sin29.6°≈0.49)
(1)求点C到直线AD的距离.
(2)将左边的门ABB1A1绕门轴AA1向外面旋转,设旋转角为a(如图3所示),问当a为多少度时,点B,C之间的距离最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于
的图象相交于![]() 、
、![]() 两点,其中点
两点,其中点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.

(1)根据图象,直接写出满足![]() 的
的![]() 的取值范围;
的取值范围;
(2)求这两个函数的表达式;
(3)点![]() 在线段
在线段![]() 上,且
上,且![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌笔记本电脑的售价是5000元/台。最近,该商家对此型号笔记本电脑举行促销活动,有两种优惠方案。方案一:每台按售价的九折销售;方案二:若购买不超过5台,每台按售价销售;若超过5台,超过的部分每台按售价的八折销售。
设公司一次性购买此型号笔记本电脑![]() 台。
台。
Ⅰ.根据题意,填写下表:
购买台数 | 3 | 10 | 20 | … |
方案一的总费用(元) | 13500 | 45000 | 90000 | … |
方案二的总费用(元) | 15000 | … |
Ⅱ.设选择方案一的费用为![]() 元,选择方案二的费用为
元,选择方案二的费用为![]() 元,分别写出
元,分别写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
Ⅲ.当![]() 时,该公司采用哪种方案购买更合算?并说明理由。
时,该公司采用哪种方案购买更合算?并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
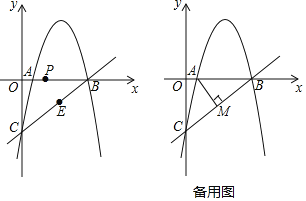
【题目】如图,抛物线![]() 经过x轴上的点A(1,0)和点B及y轴上的点C,经过B、C两点的直线为
经过x轴上的点A(1,0)和点B及y轴上的点C,经过B、C两点的直线为![]() .
.
①求抛物线的解析式.
②点P从A出发,在线段AB上以每秒1个单位的速度向B运动,同时点E从B出发,在线段BC上以每秒2个单位的速度向C运动.当其中一个点到达终点时,另一点也停止运动.设运动时间为t秒,求t为何值时,△PBE的面积最大并求出最大值.
③过点A作![]() 于点M,过抛物线上一动点N(不与点B、C重合)作直线AM的平行线交直线BC于点Q.若点A、M、N、Q为顶点的四边形是平行四边形,求点N的横坐标.
于点M,过抛物线上一动点N(不与点B、C重合)作直线AM的平行线交直线BC于点Q.若点A、M、N、Q为顶点的四边形是平行四边形,求点N的横坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com